本文最后更新于 483 天前,其中的信息可能已经有所发展或是发生改变。
【构建一个神经网络并训练它】吴恩达机器学习笔记EP6(P51-P60)

从今天开始我将学习吴恩达教授的机器学习视频,下面是课程的连接1.1 欢迎来到机器学习!_哔哩哔哩_bilibili。一共有142个视频,争取都学习完成吧。
构建一个神经网络
参考下图的神经网络架构,构建一个神经网络。
layer_1 = Dense(units=3, activation='sigmoid')
layer_2 = Dense(units=1, activation='sigmoid')
model = Sequential([layer_1, layer_2]) # 直接利用Sequential函数,将若干层按顺序串联起来,从而创建一个神经网络
x = np.array([[200.0, 17.0],
[120.0, 5.0],
[425.0, 20.0],
[212.0, 18.0]])
y = np.array([1, 0, 0, 1])
model.compile(loss=tf.keras.losses.BinaryCrossentropy()) # 定义损失函数等
model.fit(x, y) # 告诉TensorFlow这个神经网络对应的训练数据(输入和标签)
# 定义新的输入数据
x_new = np.array([[150.0, 10.0],
[300.0, 15.0]])
model.predict(x_new) # 推理

手写数字识别中更多隐藏层的示例
layer_1 = Dense(units=25, activation='sigmoid')
layer_2 = Dense(units=15, activation='sigmoid')
layer_3 = Dense(units=3, activation='sigmoid')
model = Sequential([layer_1, layer_2, layer_3])我们可以向上面这样构建多层模型,如果层数很多,我们可以简写成下面这样:
model = Sequential([
Dense(units=25, activation='sigmoid'),
Dense(units=15, activation='sigmoid'),
Dense(units=3, activation='sigmoid')])
在一个单层中的前向传播
下面是在一个单层中实现前向传播的过程。主要介绍了神经网络当中一些数据的定义方法。

前向传播的一般实现
在Numpy中实现前向传播。
用Numpy数据库构架某一层中的传播方法:
def dense(a_in, W, b, g):
units = W.shape[1]
a_out = np.zero(units)
for j in range(units):
W = W[:,j]
z = np.dot(w, a_in) + b[j]
a_out[j] = g(z)
return a_out把每一层组合起来可以构建出前向传播方法:
def sequential(x):
a1 = dense(x, W1, b1)
a2 = dense(a1, W2, b2)
a3 = dense(a2, W3, b3)
a4 = dense(a3, W4, b4)
f_x = a4
return f_x
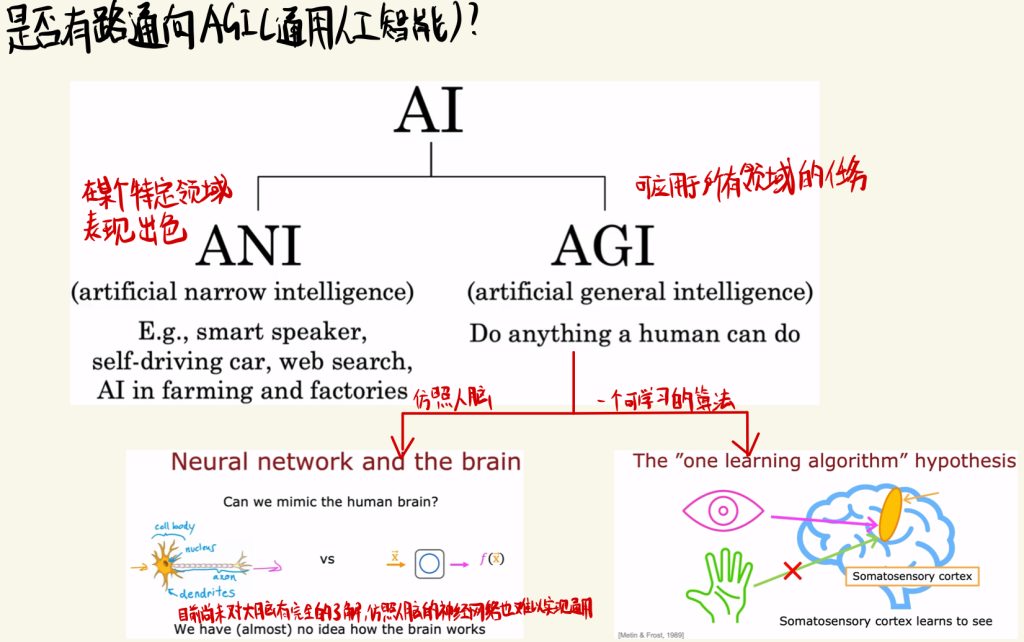
是否有路通向AGI(通用人工智能)?
AI有两个分支:在某个特定领域表现出色的ANI和可以用于所有领域任务的AGI
人们一直致力于构架一个AGI,但是目前依旧没有很好的思路。
目前主要的两个想法:
仿照人脑构建神经网络模型。但是目前人类自己对自己的大脑都了解甚少,更别说仿照人脑去构架神经网络了。所以目前神经网络只是一个叫法,其本身早已脱离了仿照人类大脑这一思路了。
还有一种方法就是构建一个可以自己学习的算法,让其自己去适应不同的数据集。
向量化,高效实现神经网络
向量化可以帮助更高效的构建神经网络。
比如dense函数的定义可以用向量化的方式更简易的构建出来:
def dense(A_in, W, B):
Z = np.matmul(A_in, W) + B # matmul由于矩阵乘法的实现
A_out = g(Z)
return A_out
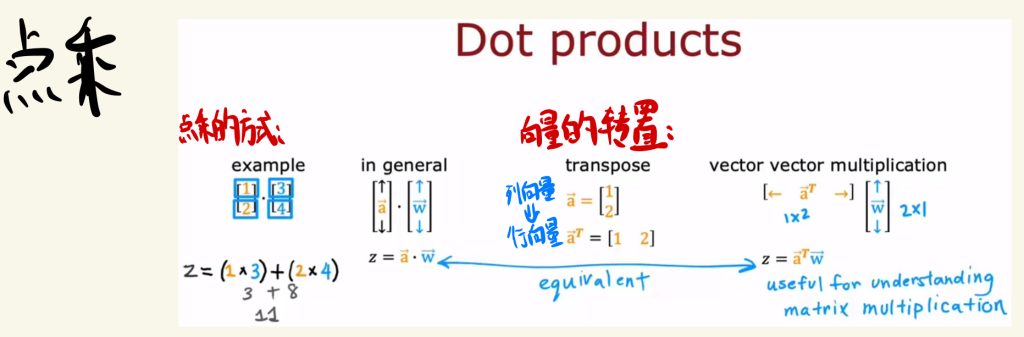
点乘
如下图是点乘和向量转置的方法:
向量和矩阵相乘
如下图是向量和矩阵相乘的方法:

矩阵乘法
如下图是矩阵乘法的方法:

矩阵乘法的规则
如下图是矩阵乘法的规则。
需要注意的是,两个矩阵相乘,前一个矩阵的列数和后一个矩阵的行数必须相同,否则无法相乘。

矩阵乘法代码
如下图是矩阵的一些定义方法。
matmul矩阵乘法也可以用@直接写。

下面是使用向量化表示一个层:
AT = np.array([[200, 17]])
W = np.array([[1, -3, 5],
[-2, 4, -6]])
b = np.array([[-1, 1, 2]])
# g用sigmoid函数的定义
def g(z):
return 1 / (1 + np.exp(-z))
def dense(A_in, W, B):
Z = np.matmul(A_in, W) + B # matmul由于矩阵乘法的实现
A_out = g(Z)
return A_out
print(dense(AT, W, b))

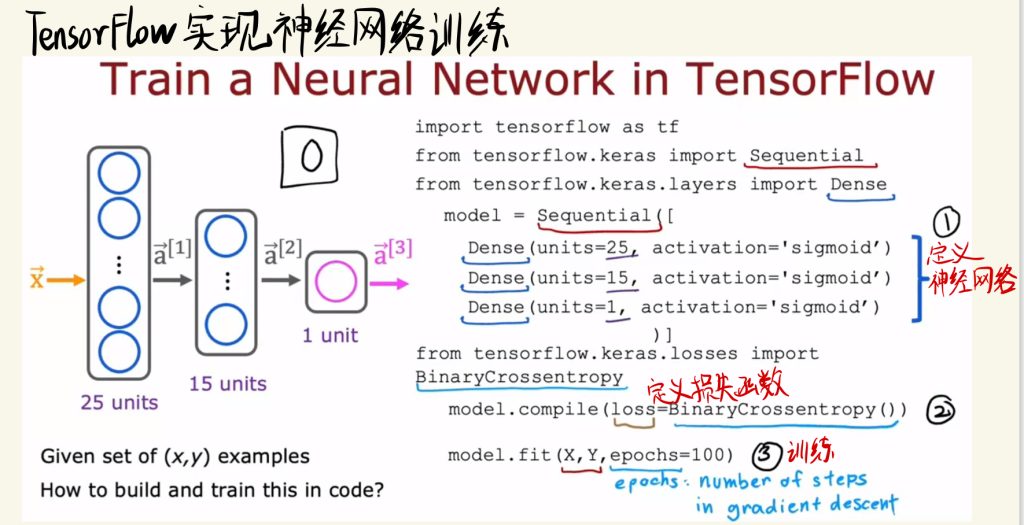
TensorFlow实现神经网络训练
下面是整个神经网络训练的简单实现代码,和上面写的差不多,这里就不重复了。
整体步骤就是先定义神经网络,然后定义损失函数等,最后进行训练。
训练细节

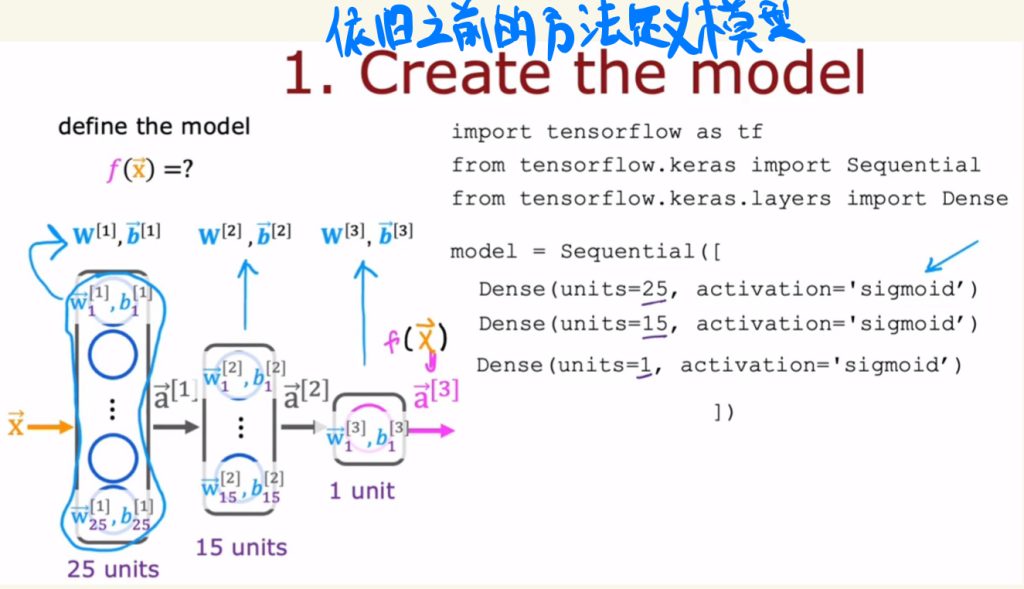
构建模型
定义损失函数和代价函数

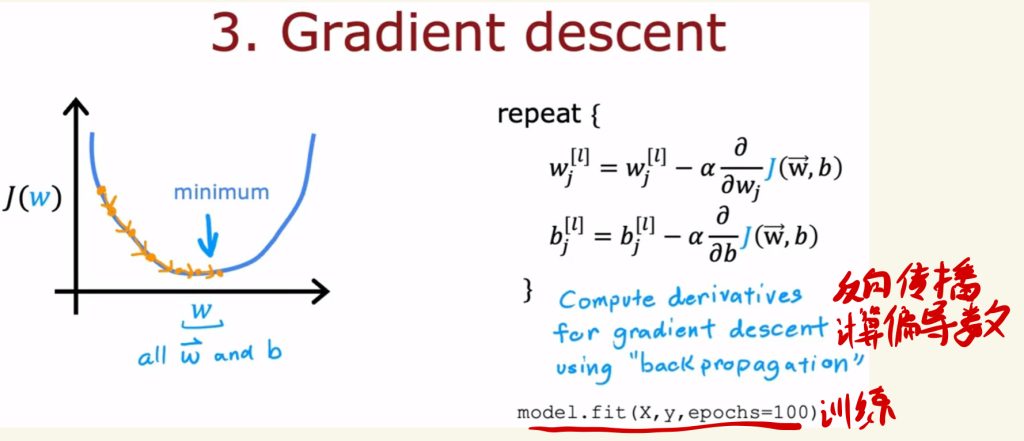
梯度下降


量好大,哥们儿!