第 1 章：数据的收集与抽样

1.1 总体与样本

1.1.1 数据

数据：可以是数字、表格、文字、语音、图片、视频

数据集 (dataset)：在特定研究中收集到的数据集合

元素(element)：数据的采集对象

变量(variable)：元素的某个特征

观测值(observation)：针对某个元素所采集的变量取值

| 数据越多并不必然意味着可以利用的有用信息越多，合理的抽样方法 (sampling method)非常重要。

1.1.2 抽样方法

总体(population)：我们研究中感兴趣的所有元素的集合

样本(sample)：从总体中抽取的部分个体形成的集合

抽样：提取过程是一种抽样。抽样方案和研究目的、目标总体 (target population) 的特点都有关联

抽样方案设计不当会导致抽样总体(sampled population) 与目标总体不一致，抽取的数据很可能带来结论性谬误

抽样总体与目标总体出现偏差，结论也就可能不正确

参数(parameter)：描述总体特征的概括性度量

统计量(statistic)：根据样本数据计算出来用于描述或估计总体特征的概括性度量。是样本的函数，不依赖于任何未知的总体参数。

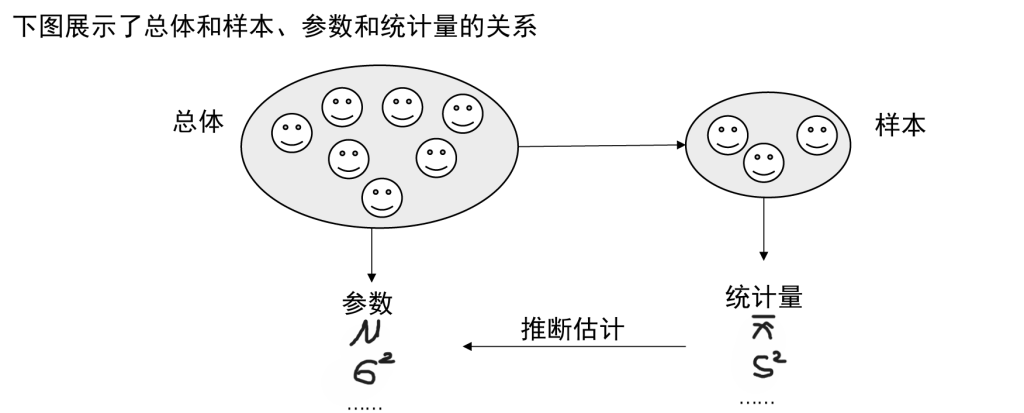
统计推断(statistical inference)： 基于样本数据对总体的特征进行推断

实验设计 (experimental design)：统计学家通过一些设计方案，从总体中抽取样本数据

观察性研究(observational study)：在已经生成的数据集中，按照某种准则抽取部分或全部样本数据进行分析

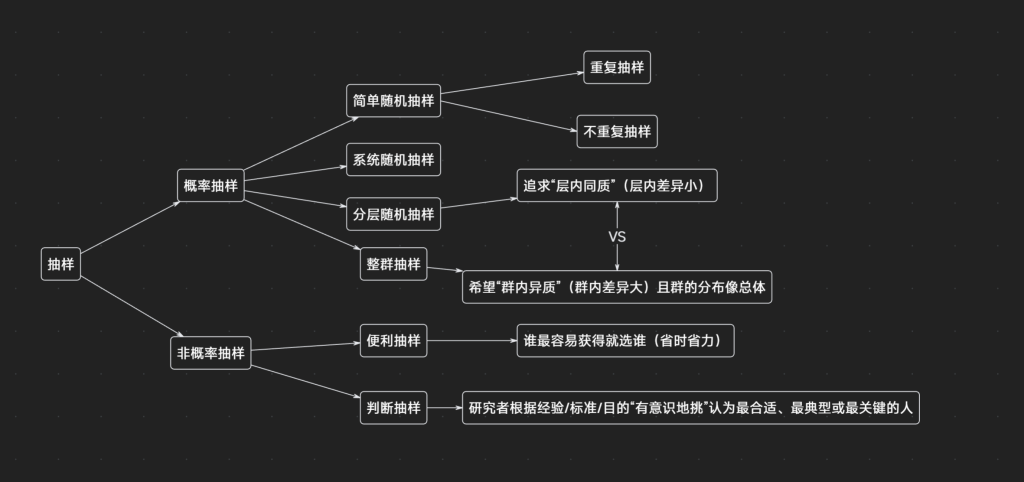
• 概率抽样：能谈“抽样误差/推断”，更正规
  • 简单随机抽样（SRS）：总体中每个元素以相同概率被独立抽取；分有放回/无放回。
    • 重复抽样：重复抽样表示一个元素被抽中之后，还有可能被继续抽取出来
    • 不重复抽样：不重复抽样则不会如此
  • 系统随机抽样：先编号，随机定第一个，再按固定间隔抽；优点是省事/经济，但若总体存在周期性会出问题。
  • 分层随机抽样：先分层（Stratum），每层内再做简单随机抽样；关键是层内差异小时质量高，且适合“不平衡组”。
  • 整群抽样（Cluster）：先分成互不相交的群，再随机抽若干个群；希望群内差异大、且抽到的群整体分布像总体时效果好。
• 非概率抽样：快，但代表性/推断能力弱
  • 便利抽样：图方便，不按概率；疫苗人体试验招募志愿者的例子：伦理上可行，但代表性可能不足。
  • 判断抽样：按研究者经验/准则挑样本（例如“两会”记者挑代表提问）。

分层 vs 整群（易混）

• 分层抽样：追求“层内同质”（层内差异小）
• 整群抽样：希望“群内异质”（群内差异大）且群的分布像总体

分层是为了更精确（控差异），整群是为了更省成本（抽一片）。

1.2 抽样方法在大数据时代的应用

海量数据分布式存储 + 隐私要求高，导致不能把数据全汇总到一起分析。

• 分布式统计推断：不合并原始数据，传递“汇总量”（例如各城市样本和）来估计参数（如正态总体的均值）。
• 当数据大到连算均值都成本高时，可以在每个节点随机抽样（如10万抽1000）来降计算成本。

第 2 章：数据的整理与可视化

2.1 数据的分类

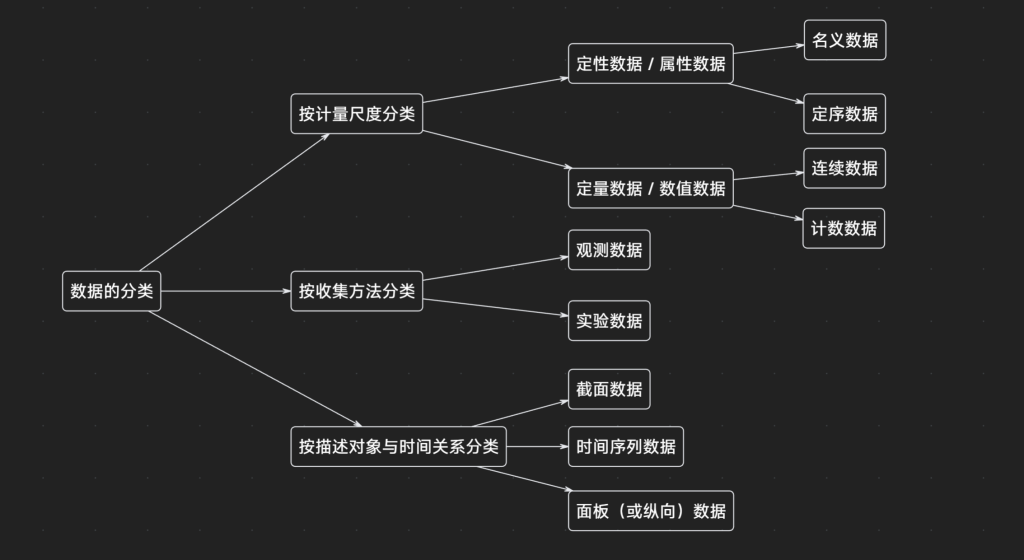
• 按计量尺度分类
• 定性数据（qualitative data）/ 属性数据（categorical data）：只能归于某一类别的非数字型数据
  • 名义数据（nominal data）：各类别之间没有序的关系。例如，性别 (男、女)、婚姻状况（未婚、已婚）等。
  • 定序数据（ordinal data）：各类别之间有序的关系。例如，文化程度（文盲、小学、初中、高中、大学）等。
• 定量数据（quantitative data）/ 数值数据（numerical data）：按数字尺度测量的数据。例如，身高、体重（连续数据），某地区每天的交通事故数（计数数据）。
• 按收集方法分类
• 观测数据（observational data）：通过调查或观测收集到的数据，无人为控制。例如，社会经济的大多数数据。
• 实验数据（experimental data）：在实验中控制实验对象而收集到的数据。例如，自然科学、医学等领域的大多数数据。
• 按描述对象与时间关系分类
• 截面数据（cross-sectional data）：在同一时间截面上收集的不同对象的数据。静态数据（同一时间，不同空间）。例如，2010年我国各省区的国内生产总值。
• 时间序列数据（time series data）：在不同时点上收集到的数据。动态数据（不同时间，同一空间）。例如，上海市过去一年的每日气温。
• 面板 (或纵向) 数据（panel/longitudinal data） / 时间序列与截面混合数据：具有横截面和时间序列两个维度（不同时间，不同空间）。例如，2010年∼2023年我国各省区每年人均国民生产总值。

2.2 数据的整理

2.2.1 定性数据的整理

对于属性数据 / 定性数据，主要汇总每一个类的频数、频率、百分比频率，以便了解频数分布和各类间的差异。

• 频数：落在某一特定类别或组中的数据个数称为频数
• 频数分布：把各个类别及落在其中的相应频数全部列出，并且用表格表示，称为频数分布
• 简单频数表：针对一个分类变量生成的频数分布表
• 列联表：根据两个分类变量生成的频数分布表，也称为交叉表

2.2.1.1 频数表

简单频数分布表如下所示：

频数频率分布表：

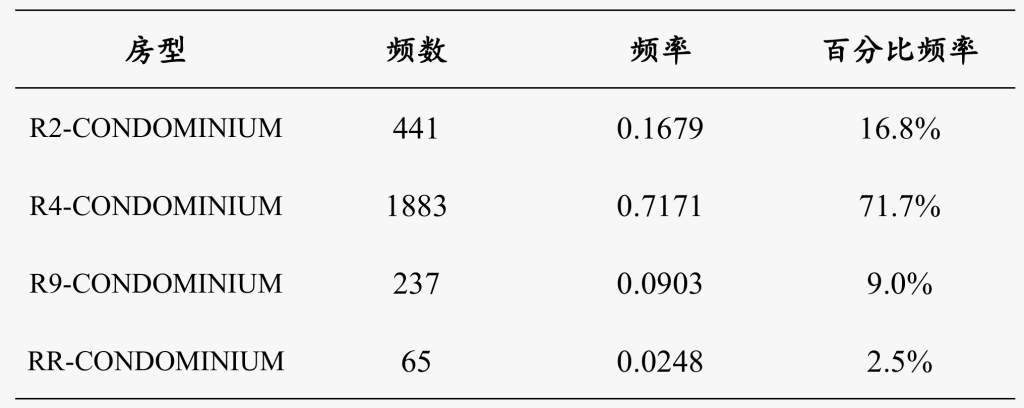
2.2.1.2 列联表

对于两个(或多个)属性数据，通过列联表（contingency table）将各个属性的交叉分类联合计数，以便了解变量之间是否存在关联性。

在两个属性数据的列联表中，两个变量分别称为行变量和列变量

如果行变量有r类，列变量有c类，交叉分类后得到的列联表称为 r × c 列联表

单元格的数值 𝑛𝑖𝑗 表示行变量第 i 类与列变量第 j 类的联合频数

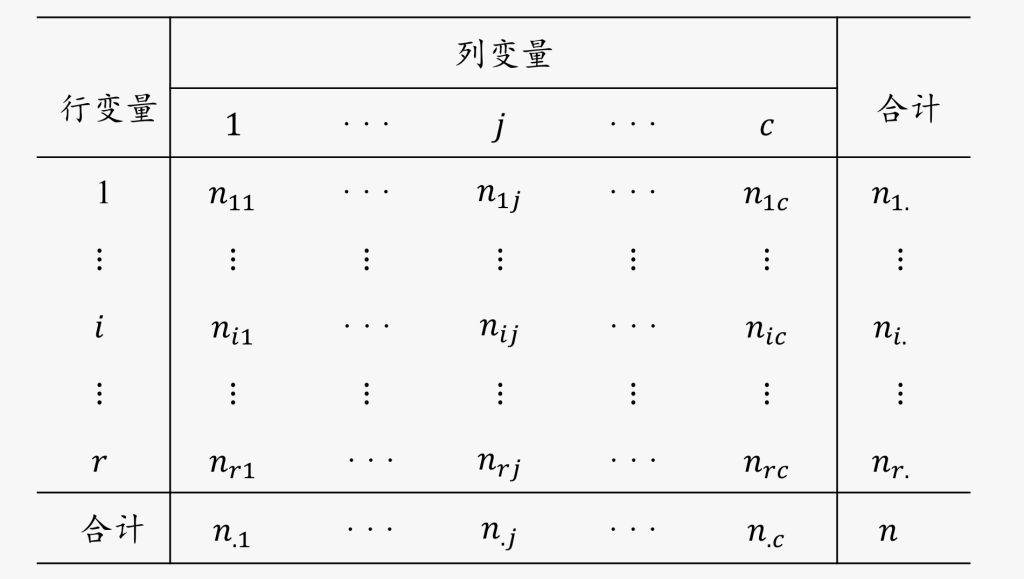
列联表经常用百分比形式表示

• 单元格频数占总数的比例𝑛𝑖𝑗/𝑛称为总和百分比
• 单元格频数占行总数的比例𝑛𝑖𝑗/𝑛𝑖∙称为行百分比
• 单元格频数占列总数的比例𝑛𝑖𝑗/𝑛∙𝑗称为列百分比

相较于计数形式，百分比列联表更容易观察变量间的关系

总和百分比列联表：

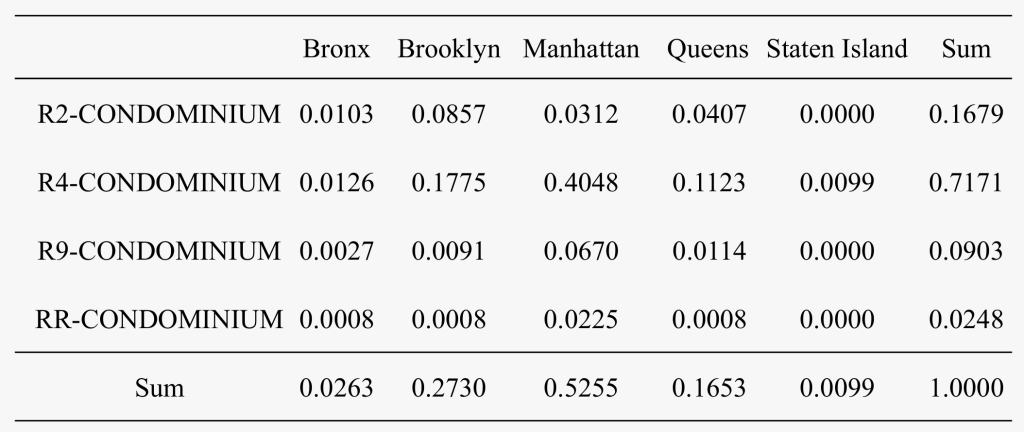
列百分比列联表：

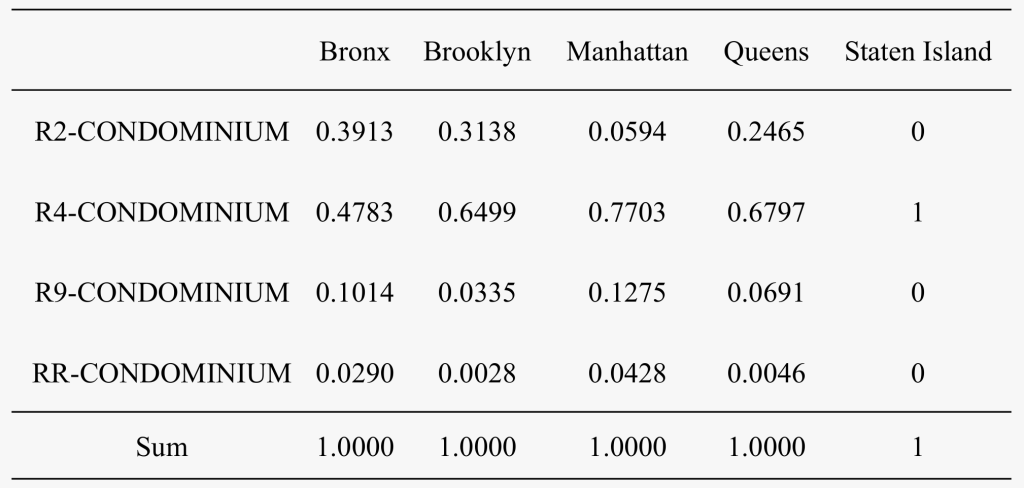
2.2.2 定量数据的整理

定量数据同样可以整理汇总成频数分布表。对定量数据编制频数分布表的一般步骤：

1. 确定区间数和区间宽度：先确定区间数，再确定区间宽度（组距） 区间数通常为 5 ∼ 20 个，区间通常取为等宽 等宽情形下，宽度可以通过“数据极差/区间数”来近似 组距 d = (最大值 – 最小值) ÷ 组数
2. 设定区间端点：第一组下限略小于最小值，最后一组上限略大于最大值，确保所有数据均被覆盖，且每个值只属于一个区间。
3. 统计频数：计算各组的频数，并列出频数分布表

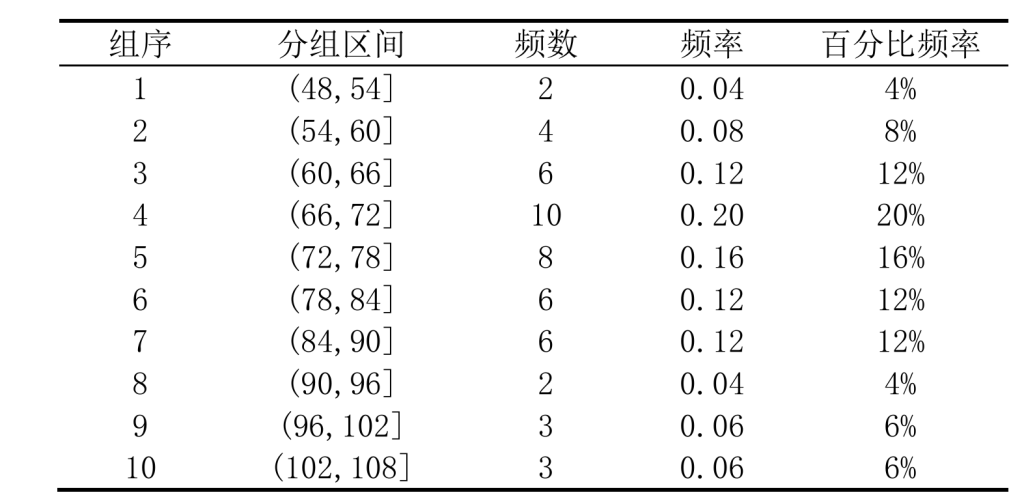
2.3 描述性度量

对于整理好的数据，通过描述性统计分析，可以挖掘出变量的很多特征，例如集中趋势、离散程度和分布形态等。

2.3.1 集中趋势的度量

集中趋势反映数据向某一中心值聚集的特性。根据中心值的确定方法，可将其指标分为两类：

• 数值平均数：利用全部数据计算得到的平均水平，主要有：
• 算术平均数、加权平均数、几何平均数
• 位置平均数：根据数据的顺序或频数确定的代表值，主要有：
• 众数、中位数、四分位数

2.3.1.1 数值平均数

算数平均数

算术平均数（arithmetic mean），简称为均值（mean）

𝑛个样本观测值 𝑥1,𝑥2,…,𝑥𝑛 的均值 𝑥 hat 定义为：

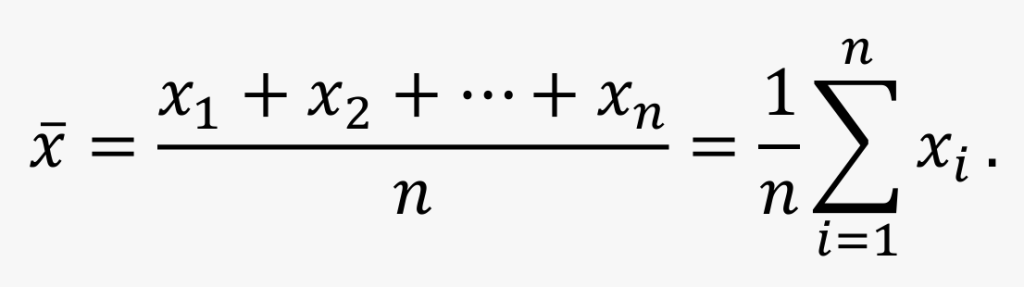
• 所有数据对均值的影响相同，权重都是 1 / n
• 均值容易受到极端值的影响

几何平均数

几何平均数（geometric mean）：𝑛 个样本观测值 𝑥1, 𝑥2,…,𝑥𝑛 乘积的 𝑛 次方根

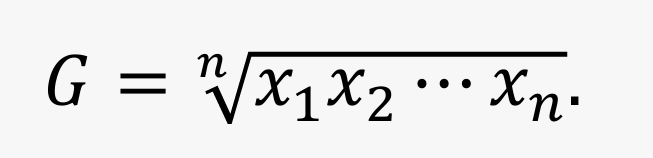
• 几何平均数常用于比率型数据，适合计算平均增长（或变化）率
• 几何平均数受极端值影响较算术平均数更小

2.3.1.2 位置平均数

众数

众数（mode）：一组数据中出现次数最多的数值

• 众数可能不唯一，也可能不存在
• 众数适用于定性数据。定量数据可能不存在众数
• 众数不易受极端值影响。

中位数

中位数（Median） ：指一组数据从小到大排序后处在中间位置的数。观测值 𝑥1,𝑥2,…,𝑥𝑛 从小到大排序之后记作 𝑥(1) ≤ 𝑥(2) ≤ ⋯ ≤ 𝑥(𝑛)，中位数为：

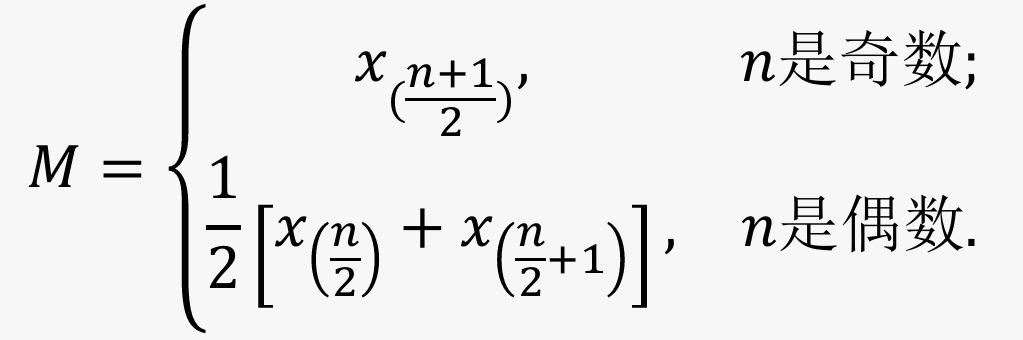
• 中位数不受极端值影响

𝒒-分位数

样本 𝒒-分位数（q-quantile）：把顺序排列的样本 𝑥(1) ≤ 𝑥(2) ≤ ⋯ ≤ 𝑥(𝑛) 进行𝒒等分的分割点对应的数值。

𝑞-分位数将数据分为 𝑞 份，共有 𝑞−1 个分割点。第 𝑘 个分割点称为第 𝒌 个 𝒒-分位数，记作 𝑄𝑘(𝑘 =1,2,…,𝑞 −1)，其定义如下：

四分位数

四分位数(quartile)：将从小到大排序后的数据四等分的三个分割点对应的数值，分别称为第一四分位数 𝑄1、第二四分位数 𝑄2（中位数）和第三四分位数 𝑄3。计算公式可以带入 𝒒-分位数的，𝒒 = 4。

例子：

2.3.2 离散程度的度量

用来衡量数据的散布程度的统计量包括：极差、四分位距、方差和标准差、变异系数等。

2.3.2.1 极差

极差(range)（也称全距）：数据中最大值与最小值之差。

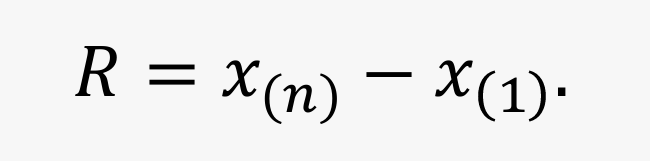
• 极差只指明了样本的最大离散范围，未利用全部样本的信息
• 优点：计算简单，含义直观，运用方便
• 缺点：易受极端值影响，且不能揭示中间数据的分布情况

2.3.2.2 四分位距

四分位距(interquartile range)：上、下四分位数之差，通常记作 𝐼𝑄𝑅。其计算公式为：

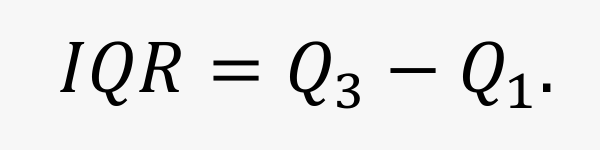
• 四分位距反映中间 50% 数据的离散程度，数值越小表示集中度越高，越大表示分散度越大
• 四分位距在一定程度上体现了中位数对数据的代表性
• 四分位距不受极值的影响

2.3.2.3 方差和标准差

方差(variance)：对于一组样本 𝑥1,𝑥2,…,𝑥𝑛，其方差 𝑠2 的计算公式为：

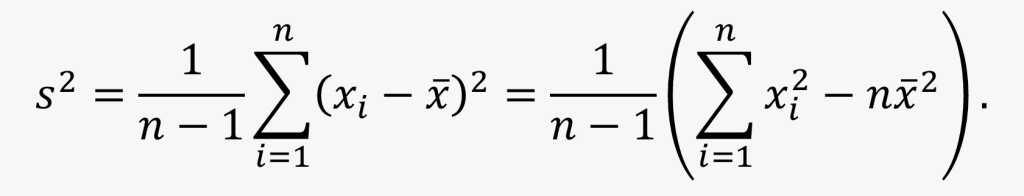
• 方差衡量数据离散程度，也是反映精确度的重要量化形式。
• 方差的单位与原始数据不一致，解释不便，因此常用方差的平方根——标准差（standard deviation，记作s）表示数据的差异程度。
• 方差为各观测值与样本均值的离差平方和的平均。
• 之所以除以 𝑛−1 而不是 𝑛，是为了在估计总体方差时更为精确（具体将在后续章节解释）。
• 方差和标准差越大，观测值分布越分散，集中趋势越弱；反之，方差和标准差越小，观测值越集中，集中趋势越强。

2.3.2.4 变异系数

变异系数(coefficient of variation)（也称离散系数）：样本的标准差与均值的比，即：

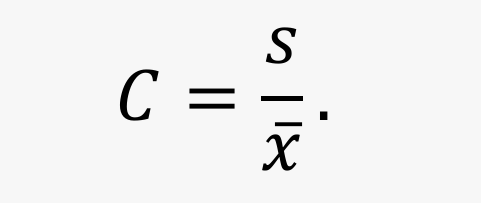
• 变异系数是一种相对离散度量，无量纲。主要用于比较量纲不同的变量，或量纲相同但均值差异较大的变量之间的离散程度
• 变异系数越大，数据越分散；越小，数据越集中
• 极差、方差和标准差属于绝对离散指标，其大小不仅受变量水平和计量单位影响，还取决于数据的变异程度

方差 VS 变异系数：

• 二者都可以描述数据的离散程度
• 均值相同时，用方差可以描述离散程度
• 均值不同时，用变异系数描述离散程度

2.3.3 分布形态的度量

偏度

偏度（skewness）：又称偏态系数，用于刻画数据分布的偏斜方向与程度，是衡量分布非对称性的统计量。

偏度定义为样本的三阶标准化矩，即：

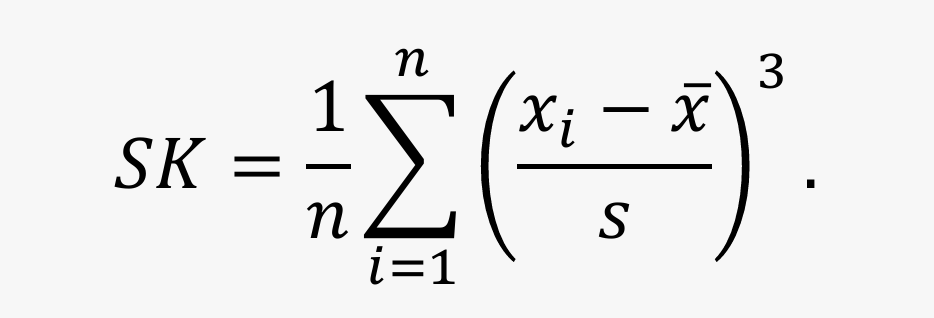
• 当 SK 接近于 0 时，数据在均值左右大致对称
  • 对于对称分布，均值与中位数应非常接近
  • 正态分布的 SK 为 0
• 当数据中存在几个明显偏大的值时，𝑆𝐾 >0
  • 从形态上看，此时分布向右延伸的程度远远大于其向左延伸的程度，我们称分布呈右偏，也称正偏
  • 对于右偏分布，由于存在极大值，均值通常大于中位数
• 数据中存在几个明显偏小的值时，𝑆𝐾<0
  • 从形态上看，此时分布向左延伸的程度远远大于其向右延伸的程度，我们称分布呈左偏，也称负偏
  • 对于左偏分布，由于存在极小值，均值通常小于中位数

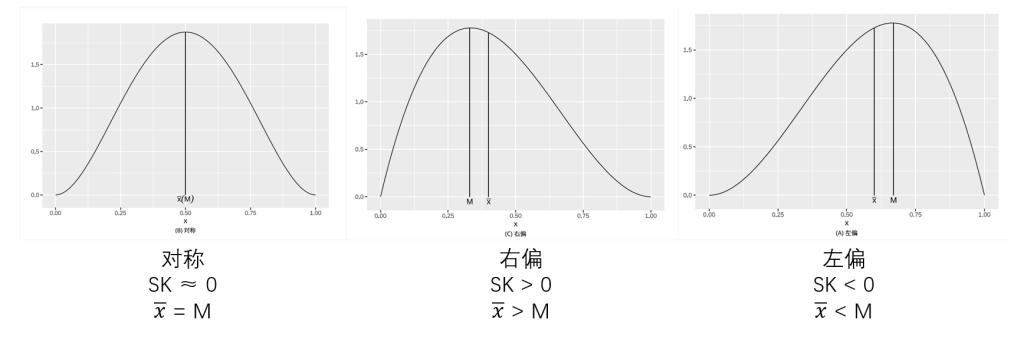
偏度描述的是分布的不对称性；“左偏/右偏”指的是哪一侧的尾巴更长（更极端、更拖尾）。

看“尾巴”不看“山峰”

峰度

峰度（kurtosis）：度量数据分布在平均值处峰值高低的数字特征

峰度定义为样本的四阶标准化矩减 3：

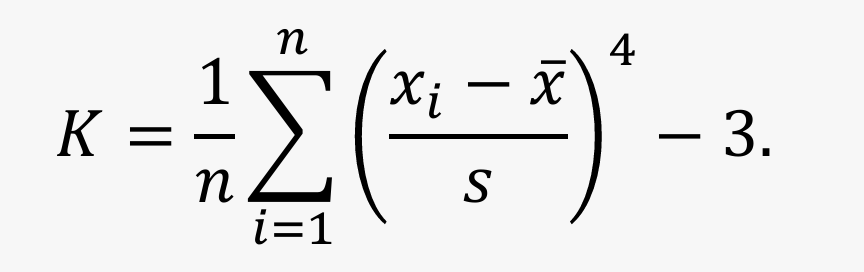
• 峰度是相较于正态分布而言的，正态分布的峰度等于 0
• 若 𝐾>0，分布较正态更陡峭，称为尖峰
• 若 𝐾<0，分布较正态更平坦，称为平峰

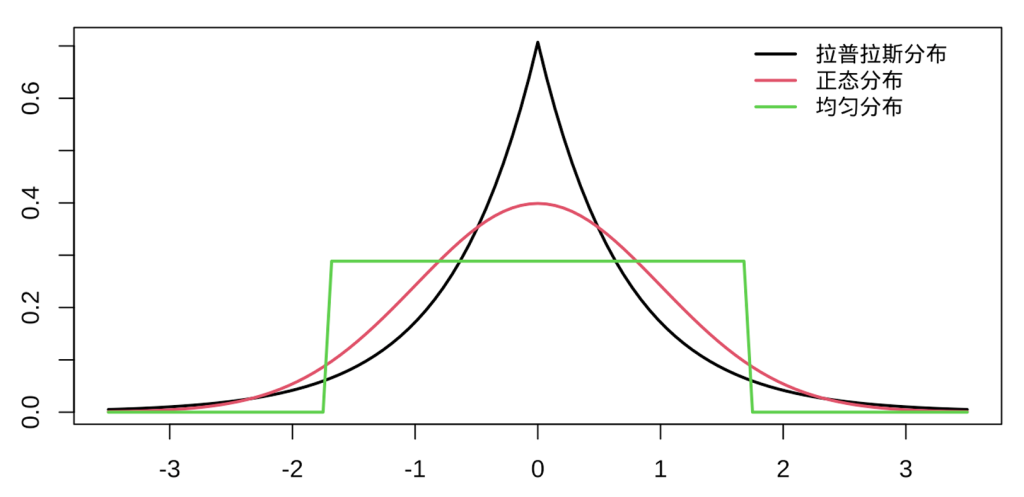
• 尖峰分布两端极值出现的概率更高，因此呈现出厚尾特征
• “峰度高”通常表现为：更尖的峰 + 更厚的尾
• 直观理解：峰度高 ≈ “更容易出现离谱值（outlier）”。
• 厚尾不是说“尾巴更长得出去”，而是说：
• 在同样离均值很远的地方，尾部概率更大 / 下降更慢。
• 上图按“尾部厚薄（极端值出现概率大小/衰减速度快慢）”从厚到薄，峰度从大到小就是：
• 拉普拉斯（黑） > 正态（红） > 均匀（绿）。

2.3.4 两个变量关系的描述

对于两个定量数据，我们可以定义样本协方差和样本相关系数来表征这两个定量变量间线性相关关系的强弱。

协方差

对于 𝑛 个样本 (𝑥1, 𝑦1), …, (𝑥n, 𝑦n)，样本协方差（sample covariance）定义为：

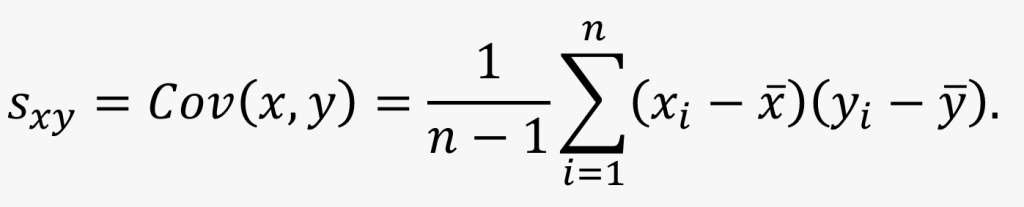
• 样本协方差是一个标量，用于描述两个变量线性关系的方向和强度：
• 若 𝑠𝑥𝑦 > 0，表示正相关关系
• 如果 𝑠𝑥𝑦 < 0，表示负相关关系
• 若 𝑠𝑥𝑦 接近 0，则说明两者几乎无线性关系
• 协方差受量纲影响较大。
• 例如，研究身高与体重时，将身高单位由米改为厘米，协方差会扩大 100 倍
• 协方差可以取任意实数，无法直接反映相关关系的强弱。 因此，统计学家皮尔逊提出了相关系数的概念

相关系数

样本相关系数 (sample coefficient of correlation)：

• 样本相关系数是数据标准化后的协方差，是剔除了两个变量量纲影响后得到的统计量
• 相关系数：
• 大于 0 表示正相关
• 小于 0 表示负相关
• 接近 0 表示无线性关系
• 相关系数的取值范围固定在 [-1,1]：
• 其绝对值越接近 1，线性相关性越强
• 越接近 0，线性相关性越弱
• 相关系数可通过统计软件（如 R 语言）计算

2.4 数据的可视化

2.4.1 定性数据的可视化

条形图

• 条形图（bar plot）
• 又称柱状图，用矩形条表示定性数据各水平，其高度对应于该水平的频数、频率或百分比，是频数分布表的图形化展示

饼图

• 饼图（pie chart）
• 以圆形为整体，按比例划分成若干扇形，每个扇形对应一个水平，其面积反映频率或百分比 在比较不同水平，尤其是频数接近时，条形图比饼图更直观清晰

南丁格尔玫瑰图

• 南丁格尔玫瑰图（nightingale rose diagram）
• 又称极坐标区域图或鸡冠花图，是弗罗伦斯·南丁格尔发明的极坐标柱状图，用以表达军队医院季节性死亡率
• 其以扇形半径表示频数或频率，由于面积与半径平方成正比，比例差异会被放大
• 适合比较数值接近的水平，若差距过大则容易夸大差异
• 因圆形具有周期特性，该图也常用于表示周期性时间数据，如星期或月份

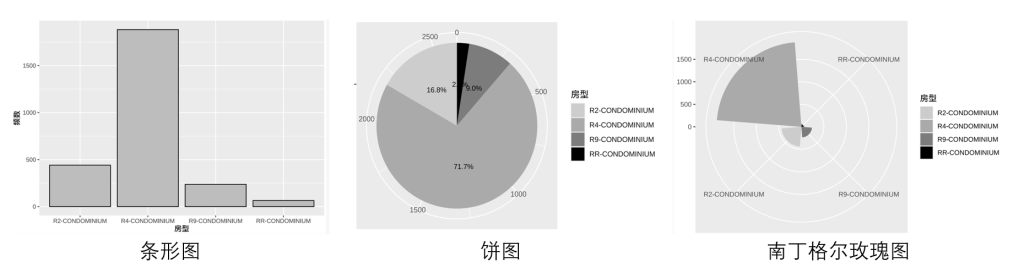
饼图 VS 南丁格尔玫瑰图：

• 相同点：
• 都把一个总体分成若干“扇形”，用来表达各类别的频数/频率/百分比。饼图里每个扇形面积反映频率或百分比。玫瑰图同样是在圆形扇区上表达频数或频率。
• 适合展示“构成结构”（谁占比更大、谁更小）。
• 不同点：
• 编码方式不同饼图靠“角度/面积”，玫瑰图靠“半径（进而面积）”。
  • 饼图：以圆为整体，按比例切成扇形，扇形的“大小”（本质上是角度/面积）反映比例
  • 南丁格尔玫瑰图：以“扇形半径”表示频数/频率；因为面积与半径平方成正比，所以差异会被放大
• 视觉效果与适用场景不同
  • 玫瑰图：更适合比较数值接近的类别；如果差距太大，容易夸大差异。另外因为圆形有周期特性，常用于表示周期性时间数据（如星期/月）
  • 饼图：当各类别频数接近时不太直观

2.4.2 定量数据的可视化

直方图

直方图 (histogram)：根据频数分布表绘制，在平面直角坐标系中以组端点为横轴、频数为纵轴，每个矩形的高度表示该组的频数、频率或百分比频率

直方图是定量数据频数分布表的图形化表示

直方图 VS 条形图：

• 条形图用于定性数据，各矩形表示不同水平，彼此离散且分隔清晰
• 直方图用于定量数据，因数据连续，各矩形相连，无明显分割
• 条形图每一矩形表示一个类别，其宽度没有意义，而直方图的宽度表示组距。

（下图第一行三张图为条形图，第二行为直方图）

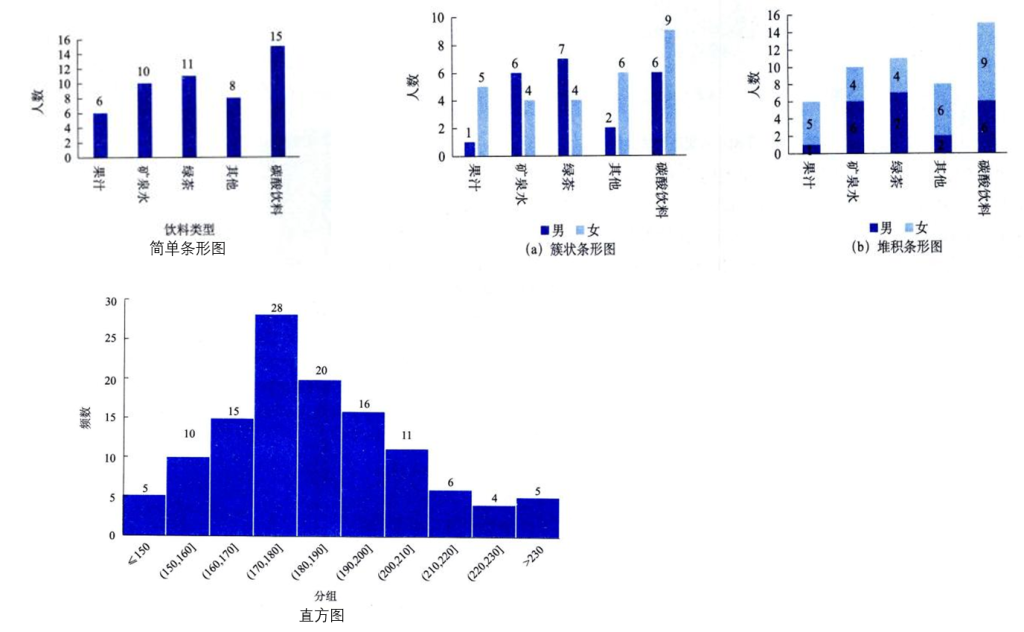
箱线图

箱线图(boxplot)：又称箱须图（box-whisker plot），基于最小值、第一四分位数（下四分位数）、中位数、第三四分位数（上四分位数）和最大值这五个统计量绘制

箱线图主要用于直观展示定量数据的分布特征，包括离散程度、对称性及异常值

• 上边缘数 = 𝑚𝑖𝑛{𝑥(𝑛), 𝑄3 + 1.5𝐼𝑄𝑅}
• 下边缘数 = 𝑚𝑎𝑥{𝑥(1), 𝑄1 − 1.5𝐼𝑄𝑅}
• 𝑄3 为上四分位数
• 𝑄1 为下四分位数
• 𝐼𝑄𝑅 为四分位距（上下四分位数之差：𝐼𝑄𝑅 = 𝑄3 – 𝑄1）
• 大于上边缘数或小于下边缘数的数据被视为异常值
• 在实际操作中，可能没有实际数据落在上边缘数或者下边缘数上
• 一般将上边缘数和其对应的须线画在不超过 𝑄3+1.5𝐼𝑄𝑅 的最大数据值处；把下边缘数和其对应的须线画在不小于 𝑄1−1.5𝐼𝑄𝑅 的最小数据值处。
• 其核心功能是观测数据的分布特征，判断分布类型：是否为对称分布（钟型）、左偏分布、右偏分布、U型分布
• 若数据左偏，则左侧离散程度更大，箱体左半部分和左须比右侧更宽
• 若数据呈对称分布，箱体左右宽度及两侧须的长度应大致相等
• 若数据右偏，则右侧离散程度更大，箱体右半部分和右须比左侧更宽

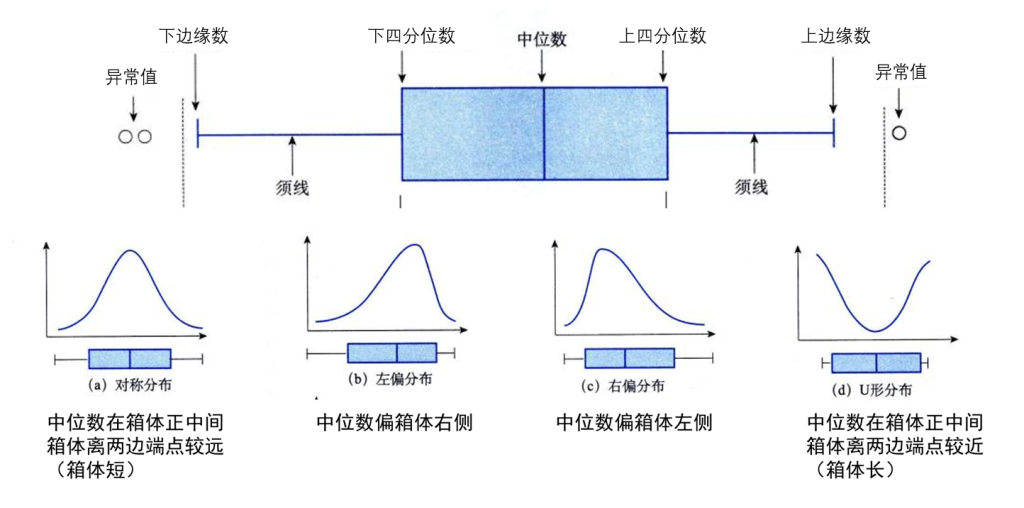
对于右偏分布的数据，常通过取对数来减弱偏态性

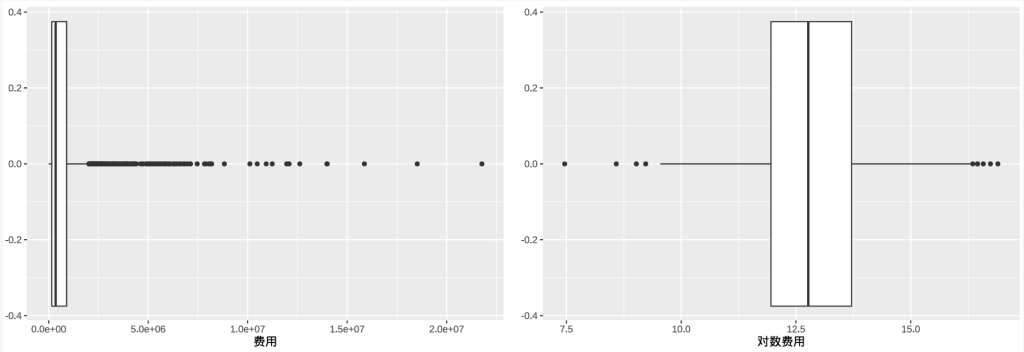
可以把多组数据画成一个箱线图

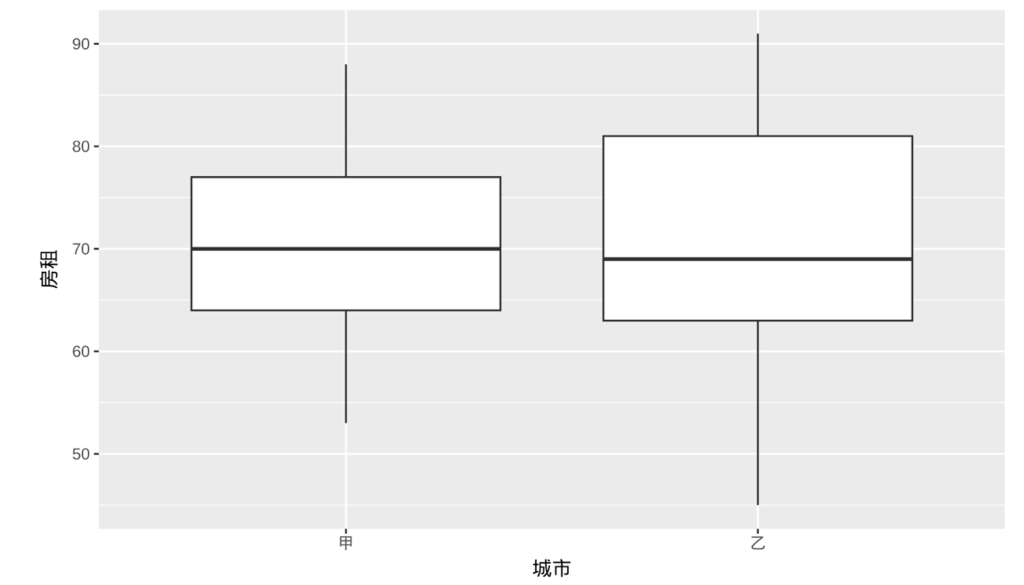
2.4.3 变量关系的可视化

2.4.3.1 两个定性变量

对于两个定性变量的关系，可使用复合条形图（side-by-side bar chart）、堆叠条形图（stacked bar chart）或南丁格尔玫瑰图。

（左：堆叠条形图；右：南丁格尔玫瑰图）

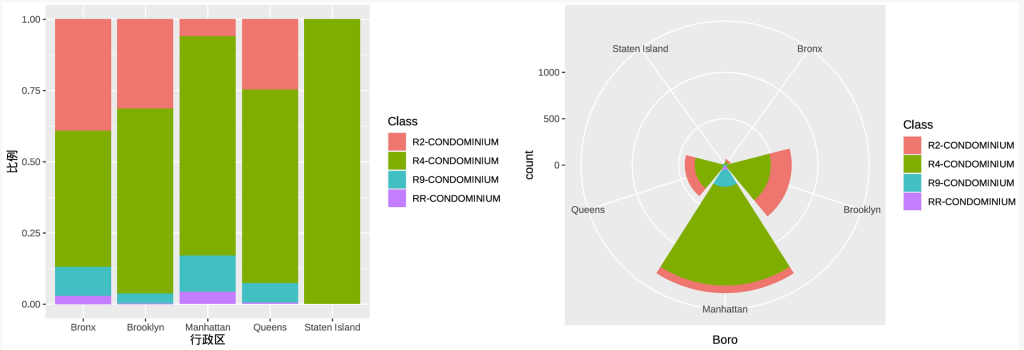
2.4.3.2 定量变量间

散点图

散点图（scatter plot）是刻画两个定量变量关系的常用图形。

它以两组数据生成一系列坐标点，通过观察点的分布来判断变量间是否存在关联或总结分布模式。

研究两个定量变量关系时，可引入定性变量进行分组比较（右）

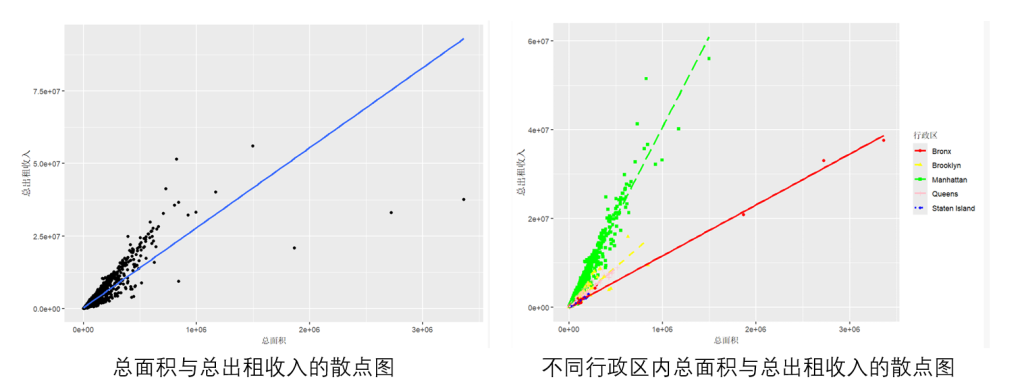
对于多个定量变量，可在 R 中用 cor 函数计算两两相关系数，并用 ggpairs 函数绘制散点图矩阵。

2.4.3.3 定性与定量变量间

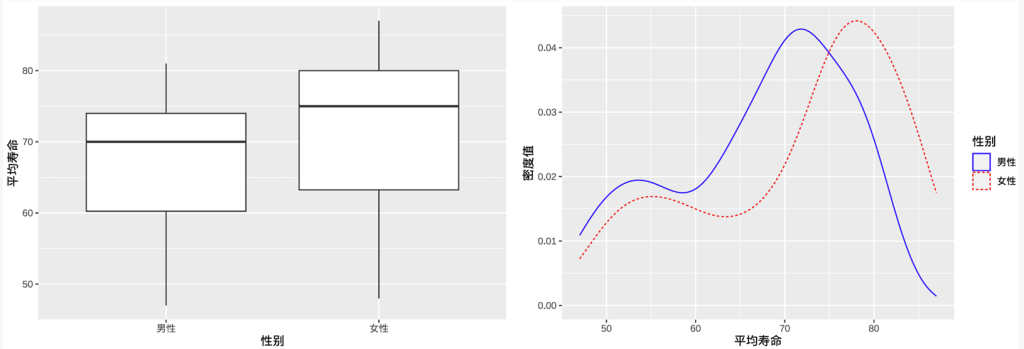
在研究定性与定量变量的关系时，常通过对定性变量分组，绘制定量变量的图形进行比较，如分组直方图、分组箱线图和分组密度图。

• 例如：性别（男/女）为定性变量，而平均寿命、人均国民总收入为定量变量