【自注意力机制】李宏毅2021/2022春机器学习课程笔记EP11(P38-P39)

从今天开始我将学习李宏毅教授的机器学习视频,下面是课程的连接(强推)李宏毅2021/2022春机器学习课程_哔哩哔哩_bilibili。一共有155个视频,争取都学习完成吧。
那么首先这门课程需要有一定的代码基础,简单学习一下Python的基本用法,还有里面的NumPy库等等的基本知识。再就是数学方面的基础啦,微积分、线性代数和概率论的基础都是听懂这门课必须的。
讲完了CNN,现在我们再来看看另外一个架构,就是自注意力机制(Self-attention)。
那之前我们都是输入一个向量进入我们的模型中,然后得到一个输出,如果输出的是一个量(Scalar),我们做的就是回归(Regression),如果输出的是一个类(Class),那我们做的就是分类(Classification)。那如果今天我们要输入的是多个向量,并且这个输入向量的数量又会时刻变化,我们又应该怎么去做呢?
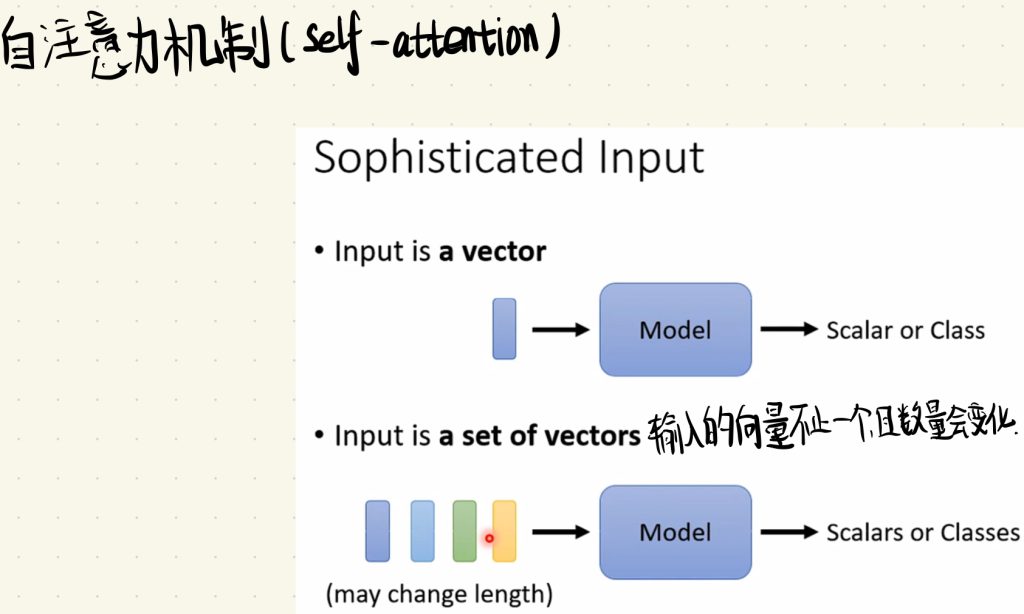
在说该怎么做之前,你可能就会有疑问:具体什么样子的情况下需要我们输入多个向量呢?
这里列举几个可能需要输入多个向量的具体问题。
1.把文字当作向量输入。比如我们做一些文本处理的时候,我们把每一个单词用one-hot编码表示成向量,然后将这些One-Hot Encoding放入我们的模型当中去处理。当然还有一种Word Embedding的方法,具体怎么做的就不在这里讲述。
2.把声音讯号当作向量输入。在HW2中我们做了语音方面的处理,比如我们就可以把一段声音讯号以10ms去切,把每一段声音讯号转化成向量在输入到模型中。值得一提的是,在做语音辨识的问题中,我们也可以参考CNN的思想,只考虑一段声音讯号中重要的部分去做判断。
3.把社交网络中每个节点当作向量输入。假如说我们去学习一个社交网络,然后给里面每个节点中的联系人根据他们的日常喜好去做广告推送。
4.把分子中的每个原子当向量输入。如果我们今天要做一个医学方面的模型,我们可以把一个分子中的每个原子元素通过One-Hot去表示。
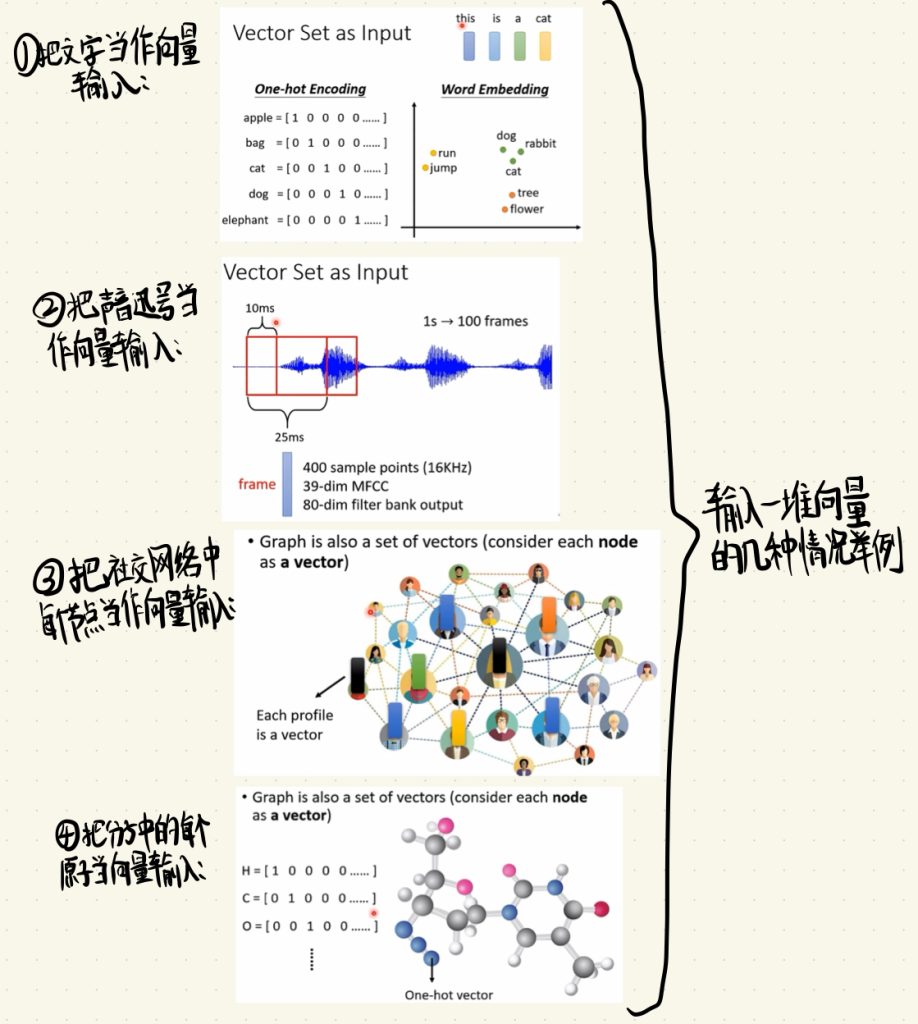
说完了几个输入的情况,我们再来看看输出可以有几种情况呢?
以下是三种可能的输出情况:
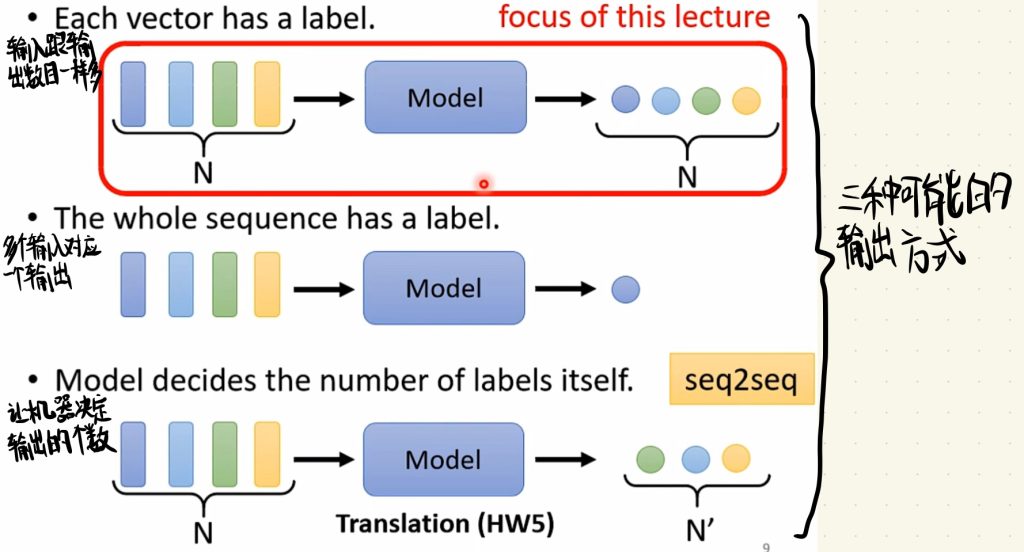
1.输入跟输出的数目一样多。这是也我们本次要探索的内容。
2.多个输入对应一个输出。
3.让机器决定输出的个数。顺便一提,这个会使用到的方法是seq2seq。
那接下去我们就来看看输入跟输出数目一样多的情况。
不同于以往只输入一个向量,这次我们需要把每一个向量分别输入到全连接层里面。
但是这里就会出现问题。假设说我们今天要做的是一个词性分类的问题,我们输入的是“I saw a saw. (我看到一把锯子)”这句话,这句话中的每一个单词我们都用One-Hot进行编码。但是这句话里的两个“saw”是不一样的词性啊,前面一个是动词,后面一个是名词。按照以往的方法,两个输入的东西都是一样的,那输出就没有道理是不同的啊。
因此我们需要一个方法去把输入的量关联起来。
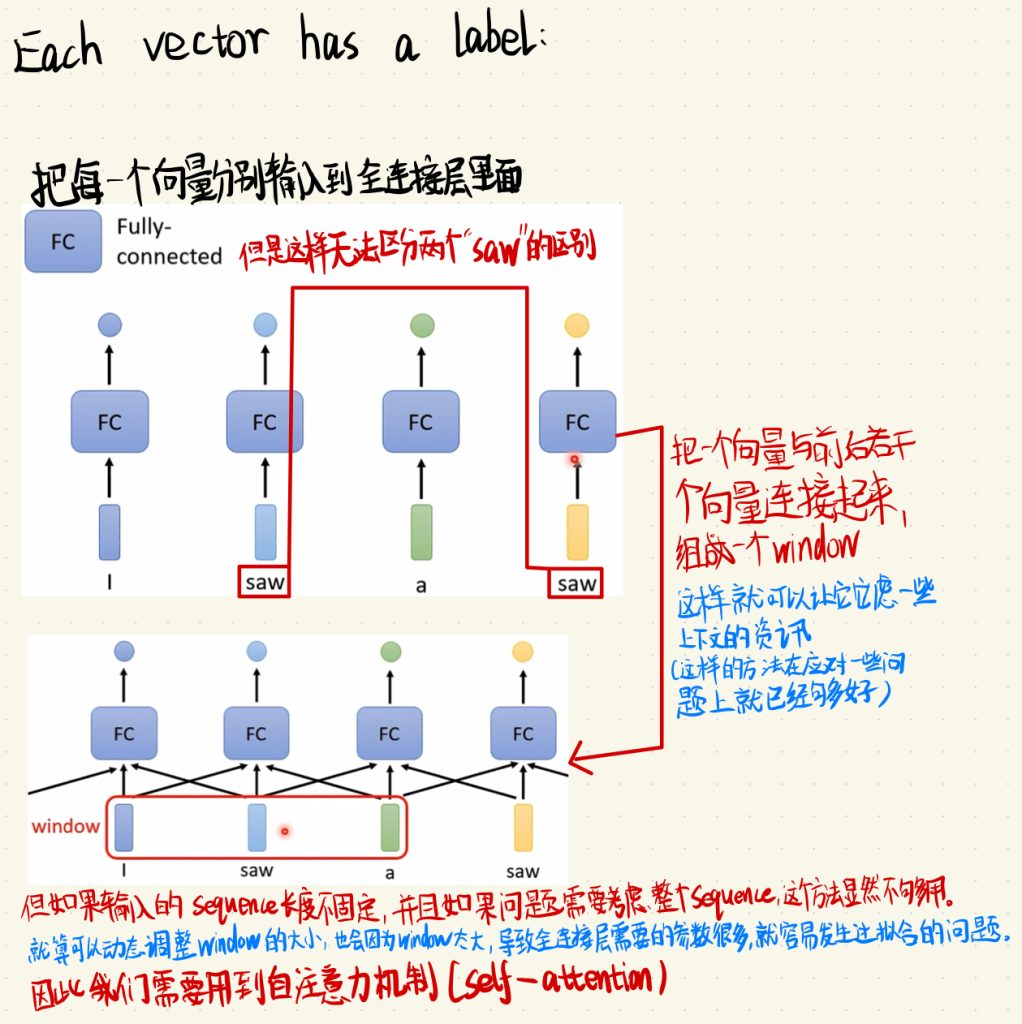
如上图这样子,我们把一个向量与前后若干个向量连接起来组成一个window。这样就可以让一个模型考虑一些上下文的咨询。实际上在这一步,我们就可以应对大部分简单的问题了。
但是如果输入的向量个数或者说Sequence长度不固定,并且如果问题需要考虑整个Sequence,这个方法显然不够用。因为就算可以动态调整window的大小,最后也会因为window太大,导致全连接层需要的参数很多,就很容易发生过拟合的问题。
因此我们需要用到自注意力机制(Self-attention)。
接下去我们就来看看Self-attention是如何运作的吧。
先来整体的看Self-attention的运行。
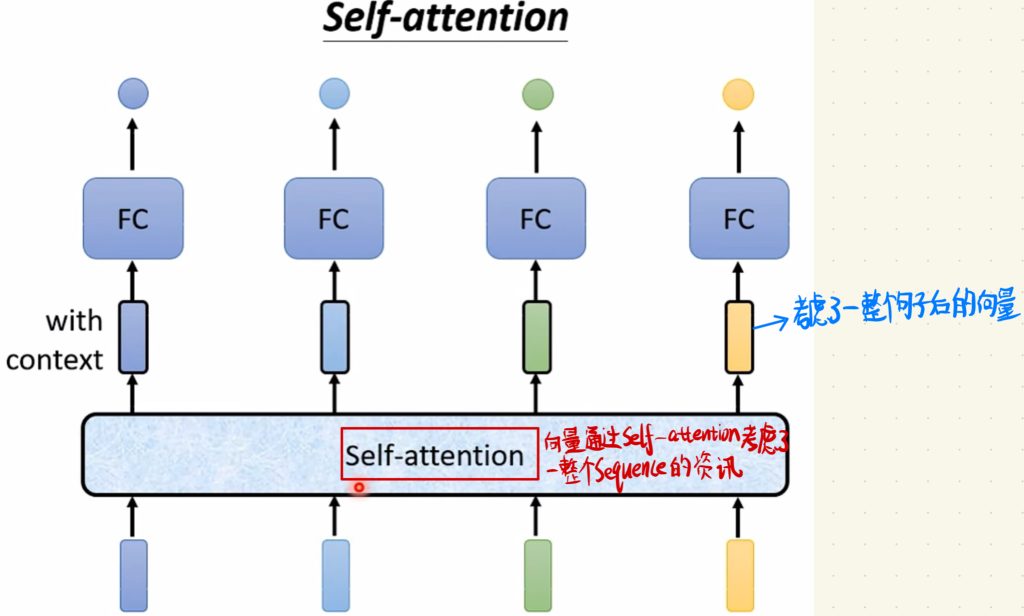
我们把一个Sequence的向量全部一起丢到这个Self-attention层里面,向量通过Self-attention层后考虑了整个Sequence的资讯,然后输入一排经过Self-attention层后考虑过一整个句子后的向量,最后我们只需要将这一排向量放到全连接层里面得到最终的输出就可以了。
当然,整个Self-attention层也可以使用多次,你可以把Self-attention层和全连接层不断重复去处理数据。
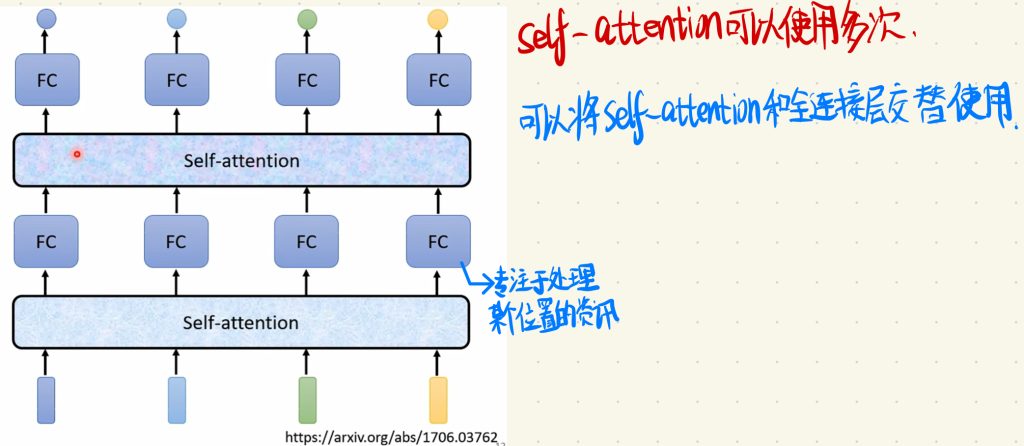
这样子,每一次进入全连接层的向量都是专注于处理某个位置的资讯了。
那接下去,我们就来看看这个Self-attention层里面是如何运作的吧。
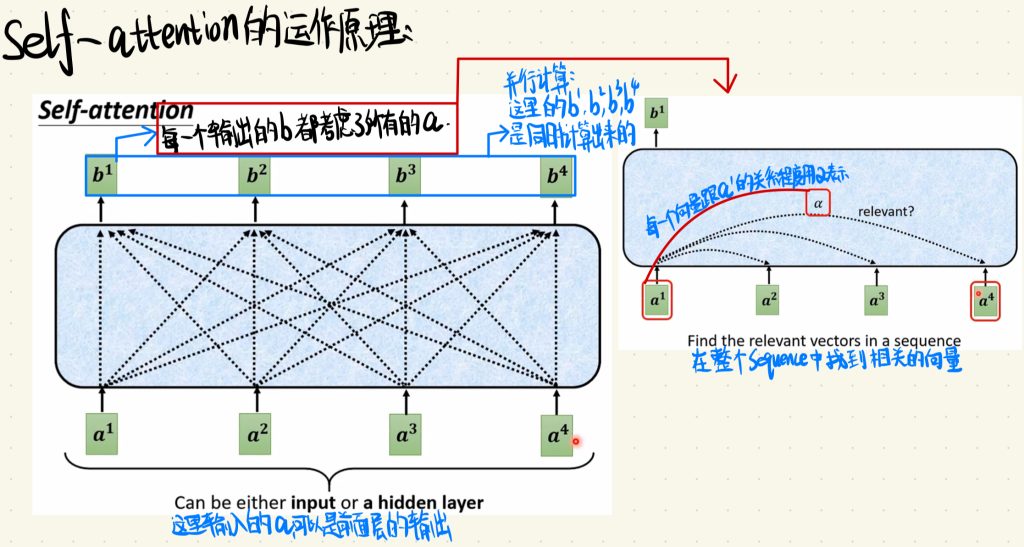
简单来说,这里每一个输出的b都是考虑了所有的输入a之后得到的。当然,这里输入的a也可以是前面层的输出。那这里输出的b是如何确定每一个a的重要性的呢?换个问法,就是这里的每一个输出b都是如何在整个Sequence中找到相关的向量的呢?
顺便一提的是,Self-attention层中计算输出b的操作是并行操作,也就是说这里的每一个输出b都是同时算出来的,这也是Self-attention很重要的一个优点,就是计算速度更加快。
答案就是:我们把每一个向量更其他向量的关系程度都算了出来,这个关系程度用α来表示。
于是,我们就来看看这个阿尔法是如何产生的。
(课上说这一段的时候说,这个方法是古圣先贤已经告诉我们的(笑))
(既然是古圣先贤告诉我们的,所以接下去就介绍方法的实现,不要问为什么这样子做。)
先把整体的流程抛出来,然后再让我们一个部分一个部分看。
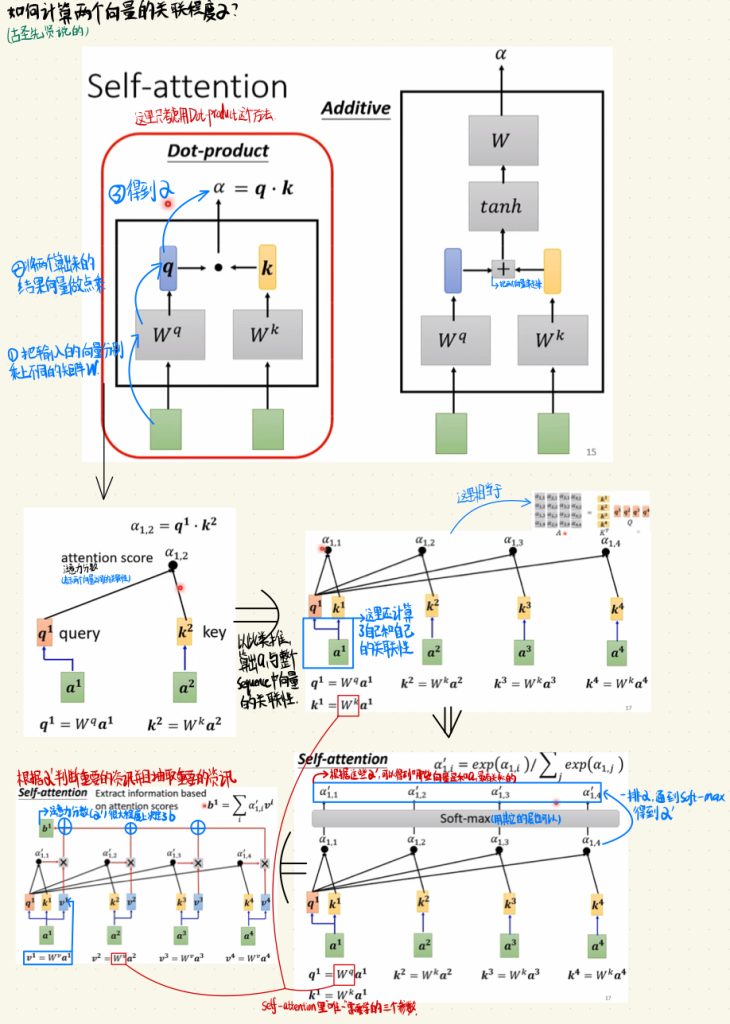
先让我们看到图中的第一个部分。
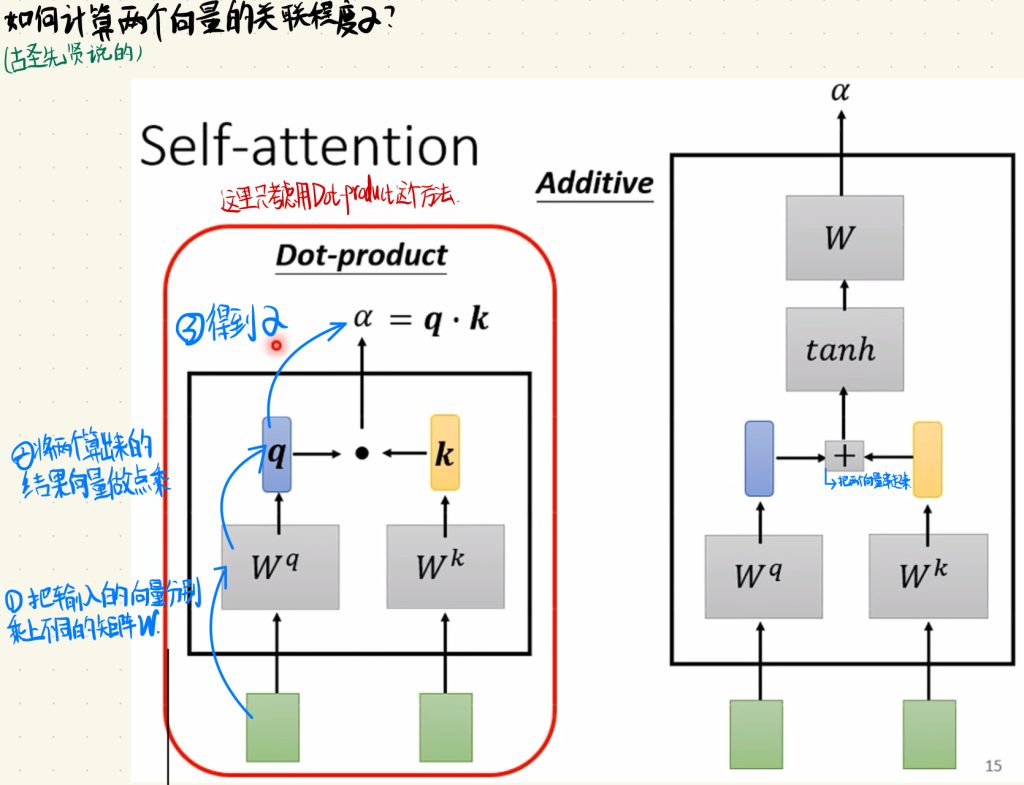
我们先说这个关联系数阿尔法的产生方法。
我们先把输入的向量分别乘上不同的矩阵W,然后将这两个算出来的结果做点乘(Dot-product),最后我们就得到了关系系数α。
这里产生α的方法不止有点乘这一种,和前面一种方法的前两步差不多,在最后的地方,我们将输出出来的向量加起来,然后通过一个tanh层。
你也可以去探寻其他产生α的方法。这里就介绍这两种,后面我们用的是第一种点乘的方法。
当然看到这里,你可能也会有和我一样的疑问,就是这个矩阵W到底是什么?
这个W在之后其实会解释,这里讲述的时候只说乘上一个矩阵W确实有点突兀,导致一开始我听课的时候也有点懵。所以,先来剧透一点点后面的内容。就是这个矩阵是什么,这个矩阵W其实是我们需要学习的参数而已。接下去还有很多成矩阵W的地方。
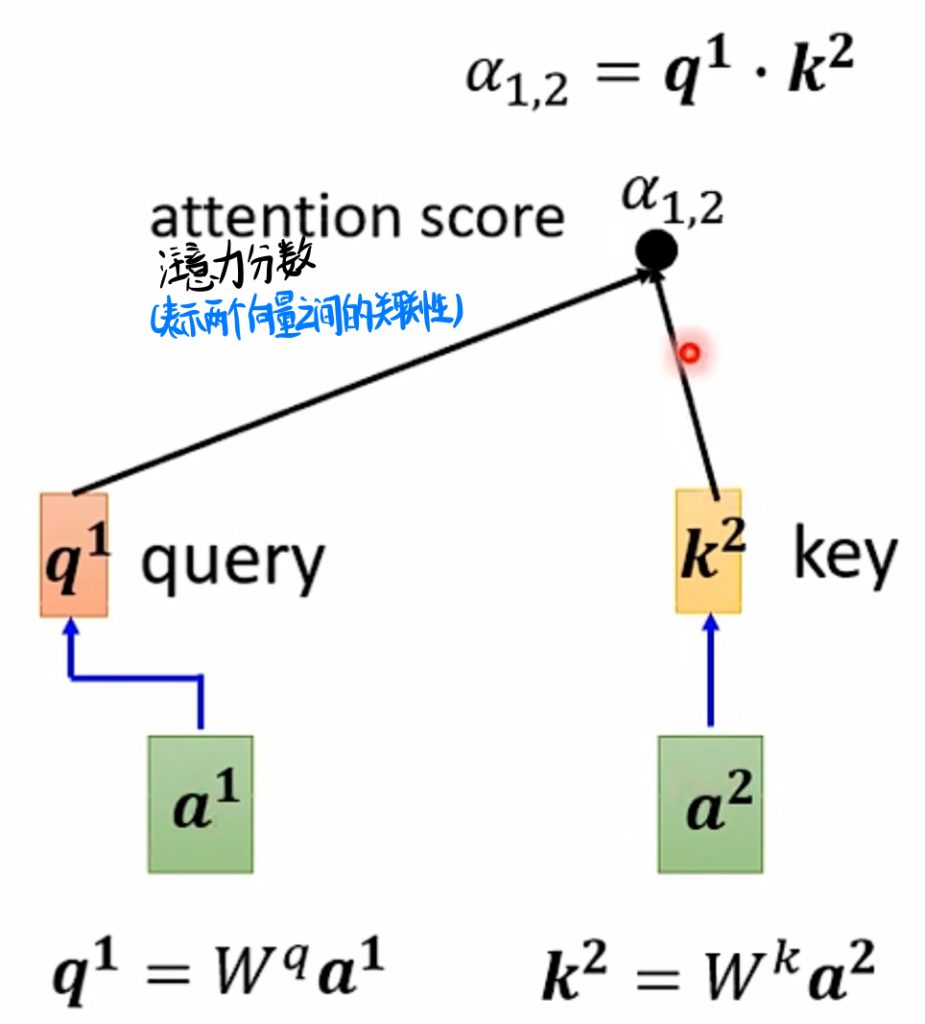
我们换种方式来解释这个α是如何产生的,就是先把要处理的a1乘上一个矩阵Wq,得到一个向量q1,那这个q1有一个专有的名词query。然后这个Sequence的其他剩余向量乘上一个矩阵Wk得到一个k2,这个k2也有一个专有的名词叫key。那这个α我们也给一个专有名词叫注意力分数。比如上图中,我们就计算出了a1和a2这两个向量的关系,我们记作α1,2。
以此类推,我们就可以求出a1跟整个Sequence中向量的关联性。
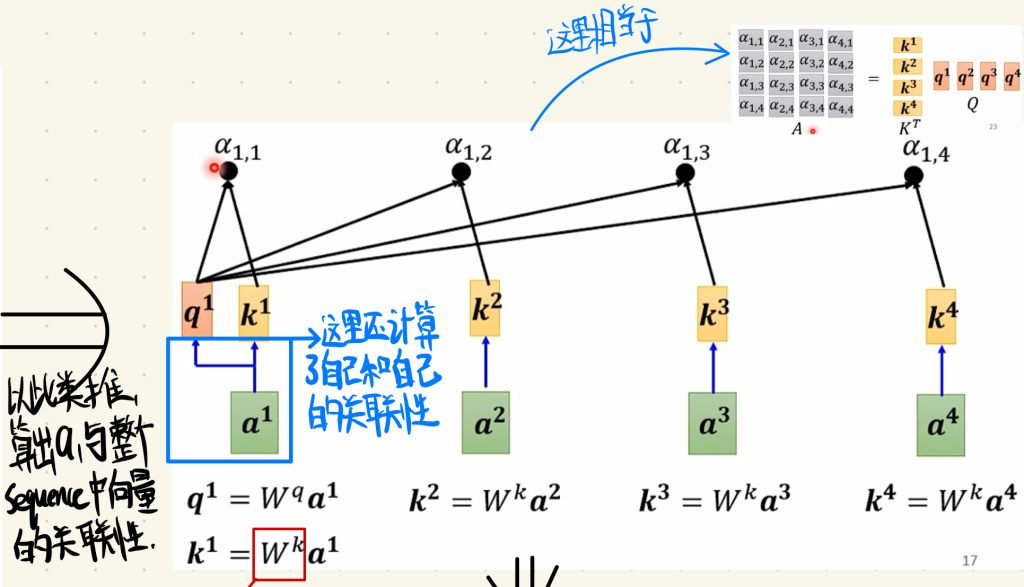
值得注意的是,这里我们还把a1跟自己的关联性也考虑了进来。当然求α这步操作也可以写成两个向量之间相乘得到所有α的矩阵,里面是所有两个输入向量之间的注意力分数。
接着,我们还可以对这些注意力分数α做处理。
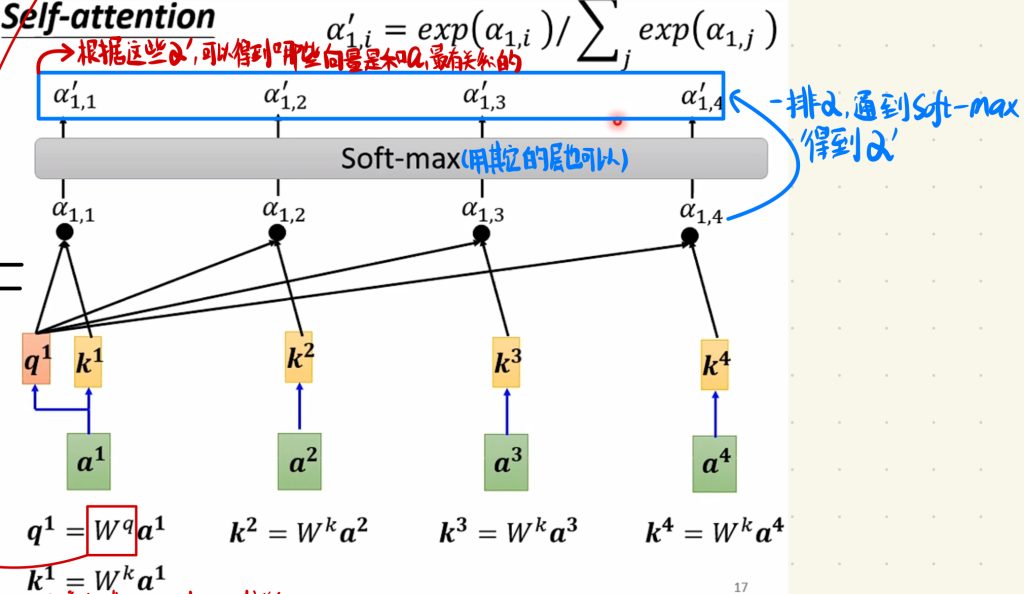
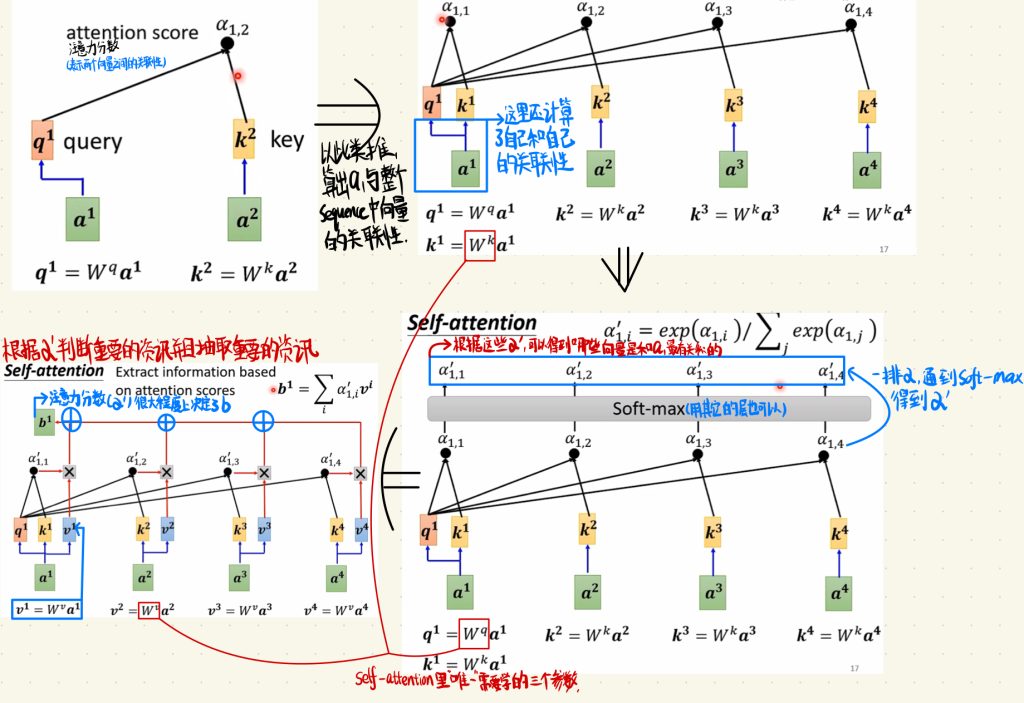
我们可以把输出的α再过一次Soft-max层,当然你用其他的层都是可以的,只是Soft-max层在这更加常见。
最终通过Soft-max层后,我们得到一排α’,根据这些α’,可以得到哪些向量是和a1最有关系的。
接着看最后一步。
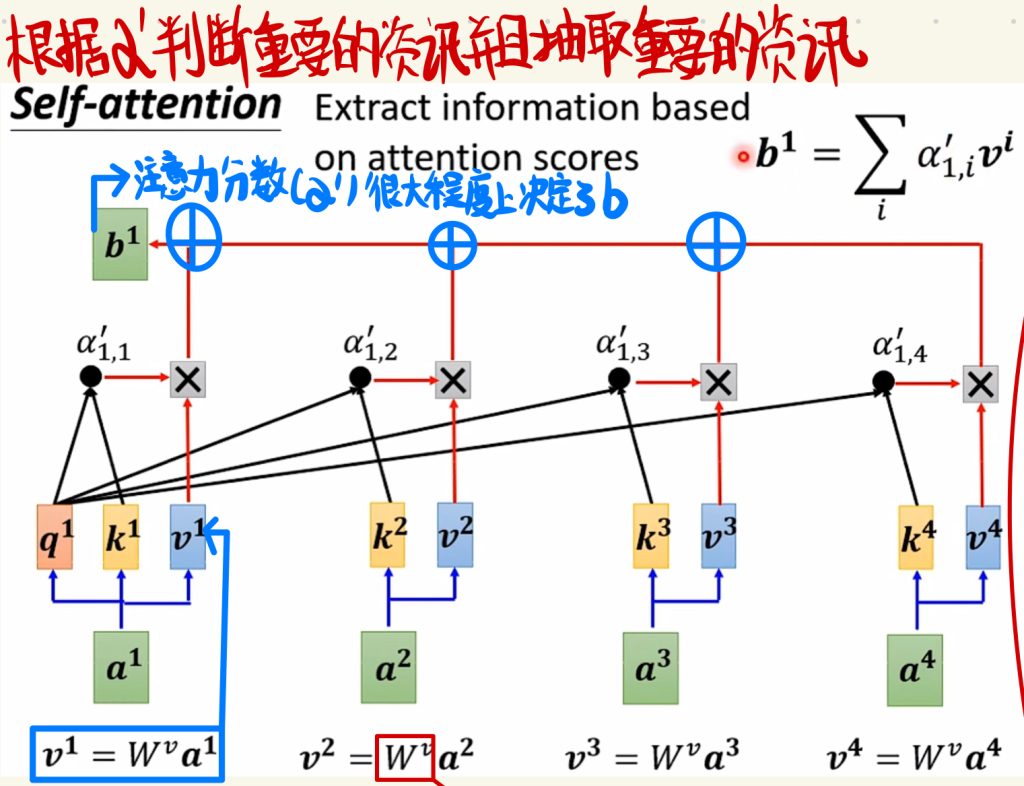
也就是说Self-attention层中根据α’判断重要的资讯,并且抽取重要的资讯。最后我们再引入一个需要学习的矩阵Wv,我们再将所有的输入a乘上Wv得到一个向量v。最后,我们将这个向量v乘上每一个分别的相关系数,最后把每一个算出来的结果全部加起来,就得到了一个输出b。从这里我们也不难看出,最终的输出结果和这个注意力分数α’有着很大的关系,也就是说,注意力分数α’很大程度上决定了输出b。
说完了这么复杂的计算流程,我们再回过头看看整个的训练过程,其实就会发现,Self-attention层中“唯一”需要学习的就只有三个参数矩阵。
相关这件事情啊,它也有很多不同的形式,有很多不同的定义。所以,也许我们不止要有一个q(query)去表示不同种类的相关性。这个时候,我们就需要多头注意力机制。
这里我们用2head举例,更多的数量也一样。
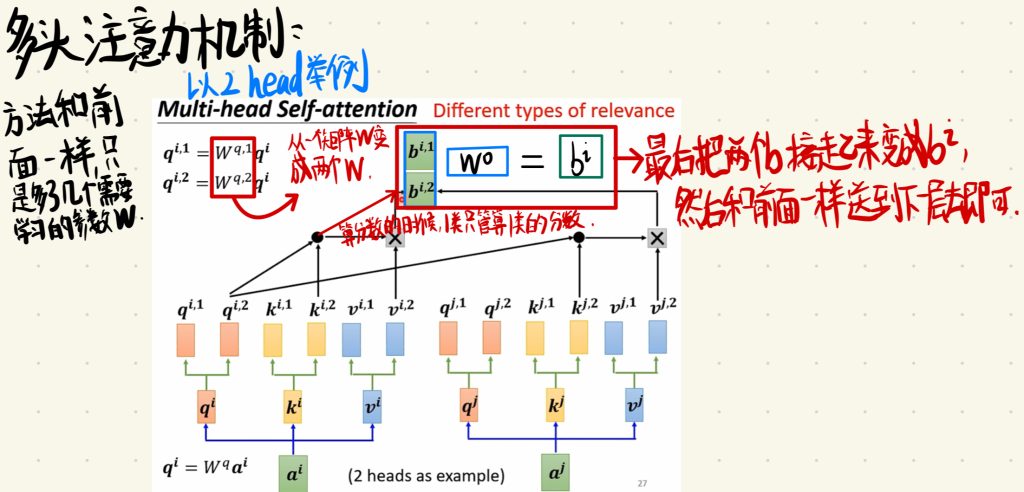
那方法其实也跟之前的一样,只不过这里多了几个需要学习的参数W。也就是从一个矩阵W,变成了两个W。然后算分数的时候,每一类特征只管算自己这一类的分数即可。最后我们会得到两个输出b,我们只需将这两个b连接起来变成bi然后和前面一样送到下一层即可。
在处理一些特殊的问题当中,比如词性判断中可能需要位置的资讯,于是我们就可以把位置的信息也放入Self-attention中。
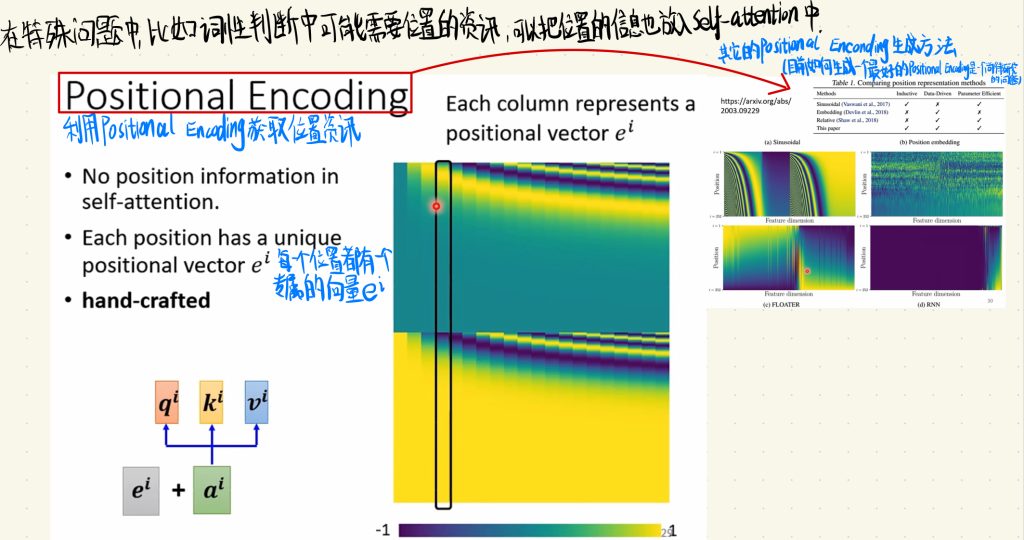
我们可以利用Positional Encoding去获取位置资讯,每一个位置都有一个专属的向量ei。然后这个Positional Encoding的生成方法有很多,比如FLOATER、RNN等等,但是每一种生成方法都有自己的局限性,目前如何生成一个最好的Positional Encoding任然是一个尚待研究的问题。
然后Self-attention也可以用于语音辨识的问题当中。
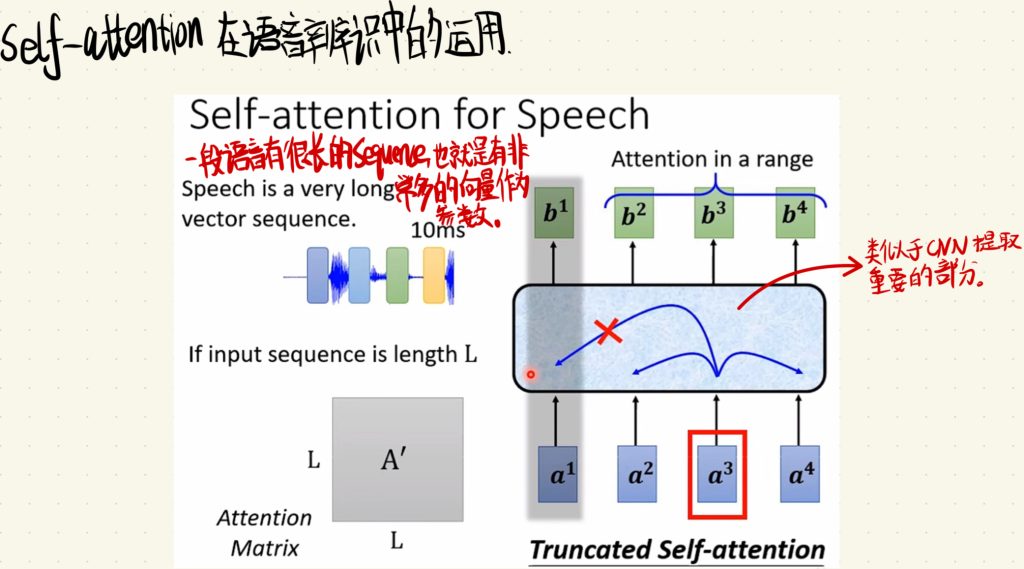
一段语音有很长的Sequence,也就是有非常多的向量作为参数输入,这很符合我们这一次使用的方法。当然,一段语音的参数很多,我们需要借助类似CNN特征提取的思想,只输入重要的部分。
然后Self-attention同样可以使用在影像处理上面。
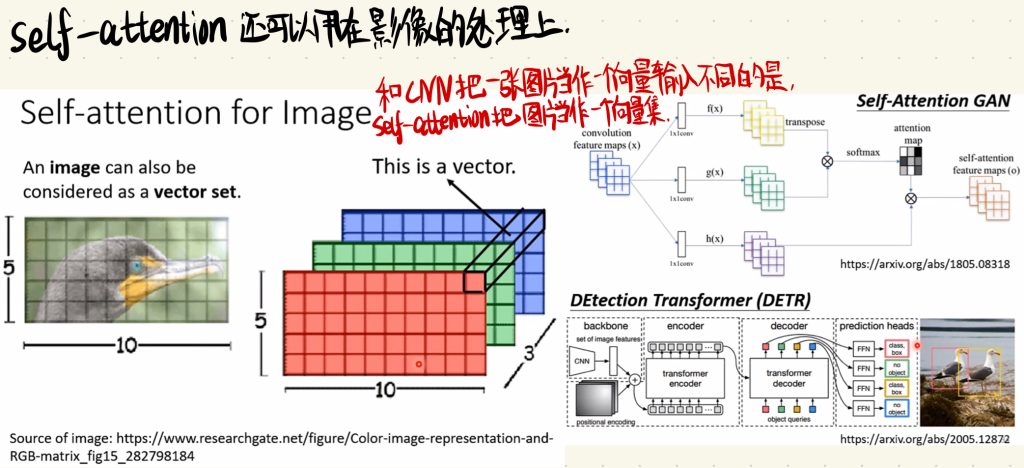
在CNN当中,我们将一张图片处理成一个向量输入到全连接层当中。和CNN不同的是,Self-attention把图片当作一个向量集(Sequence)去处理。最后利用Self-attention也依旧可以达到我们的目的。
于是我们就来比较一下CNN和Self-attention的区别。
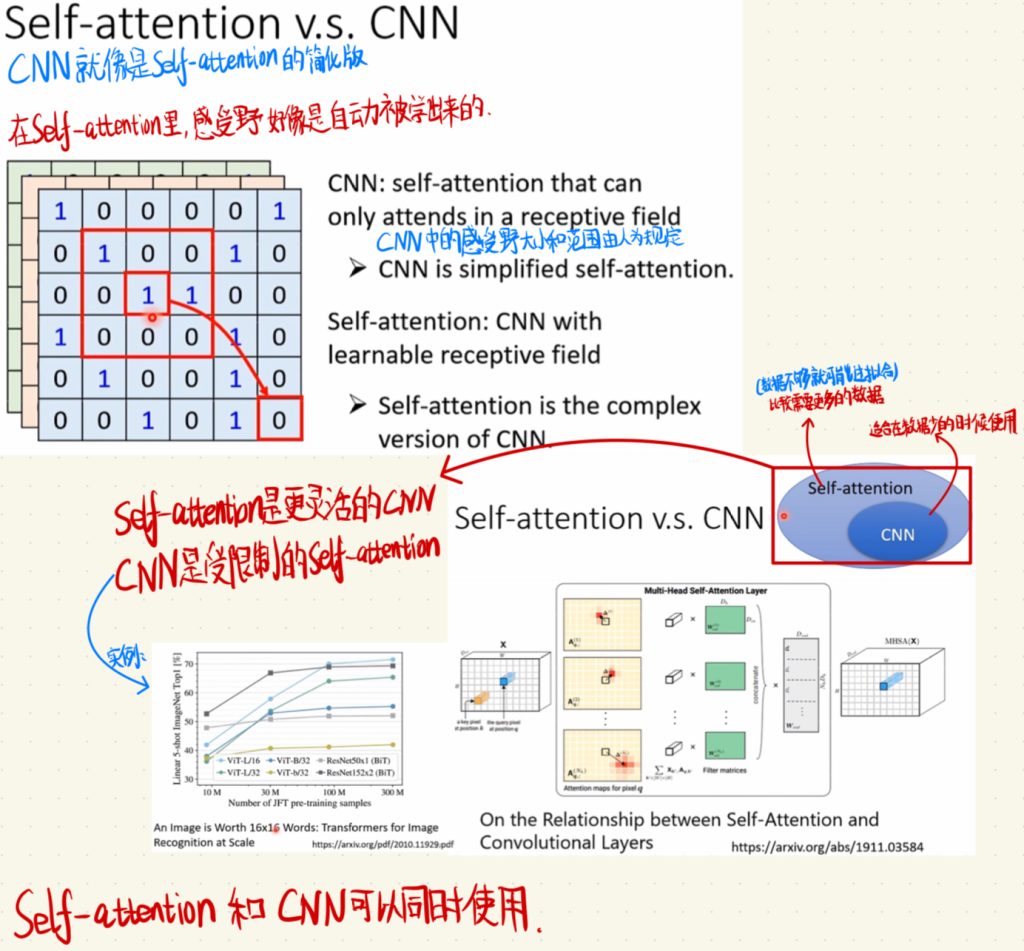
简单来说,CNN就像是Self-attention的简化版。Self-attention是更灵活的CNN,反过来说,CNN是受限制的Self-attention。在CNN中,感受野的大小和范围由人为规定。而在Self-attention中,CNN里面讲的感受野就好像是自动被学出来的。画图的话就是,Self-attention中包含了CNN。但是Self-attention需要更多的数据,如果数据不够就可能发生过拟合,而CNN的好处是适合在数据少的时候去使用。
当然,你也说我全都要。Self-attention和CNN也可以同时被使用。
RNN是一个循环神经网络,在这里我们不会详细的去讲RNN,看到后面就会告诉你原因。
我们再来对RNN和Self-attention做个比较。
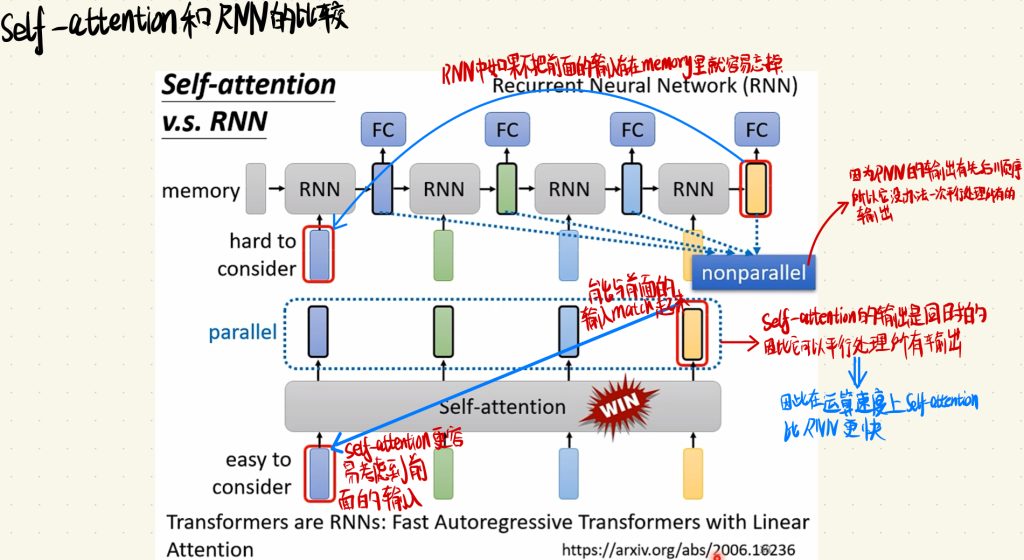
RNN是输入一个数据,然后通过RNN层,将输出给到全连接层,然后再输入一个数据,再通过RNN,然后RNN会考虑一次周围输入的参数再给出输出,接着再把这个输出放到全连接层当中,然后再输入一个数据,以此类推。但是这样子的话,RNN中如果不把前面的输入存在memory里,它就容易忘掉。因为RNN的输出有先后顺序,所以它没有办法一次平行处理所有的输出。而通过前面对Self-attention的介绍,我们就不难看出,Self-attention更容易考虑到前面的输入,它能与前面的输入配对(match)起来。因为Self-attention的输出是同时的,因此它可以平行处理所有的输出,也就是说在运算速度上Self-attention也比RNN更快。
更具前面的比较,Self-attention完胜RNN。因此,在今天我们说Self-attention是可以完美替代RNN的,这也就是前面为什么说不需要详细了解RNN的原因。
最后Self-attention还可以用在图表中。
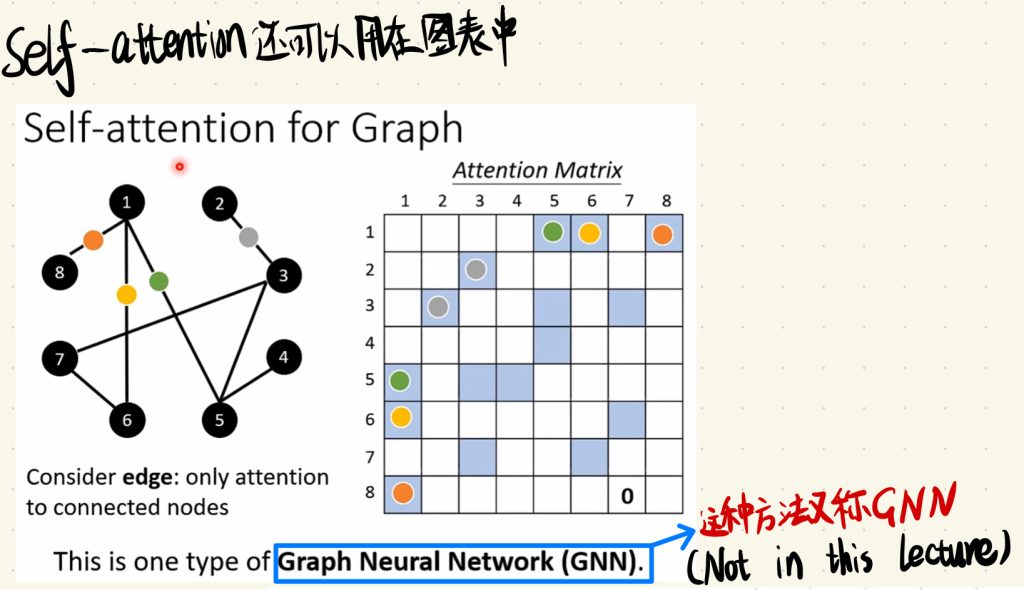
值得一提的是,这种处理Graph的方法又称为GNN。这个就比较复杂了,在这一次的课中没有提及。
我们了解了Self-attention的机制之后,我们还是会觉得Self-attention的计算量仍旧非常大,这也就出现了各种对Self-attention的改进。比如Self-attention最早就是用于Transformer上面。很好玩的是,后来所有的Self-attention改进都叫做xxformer。
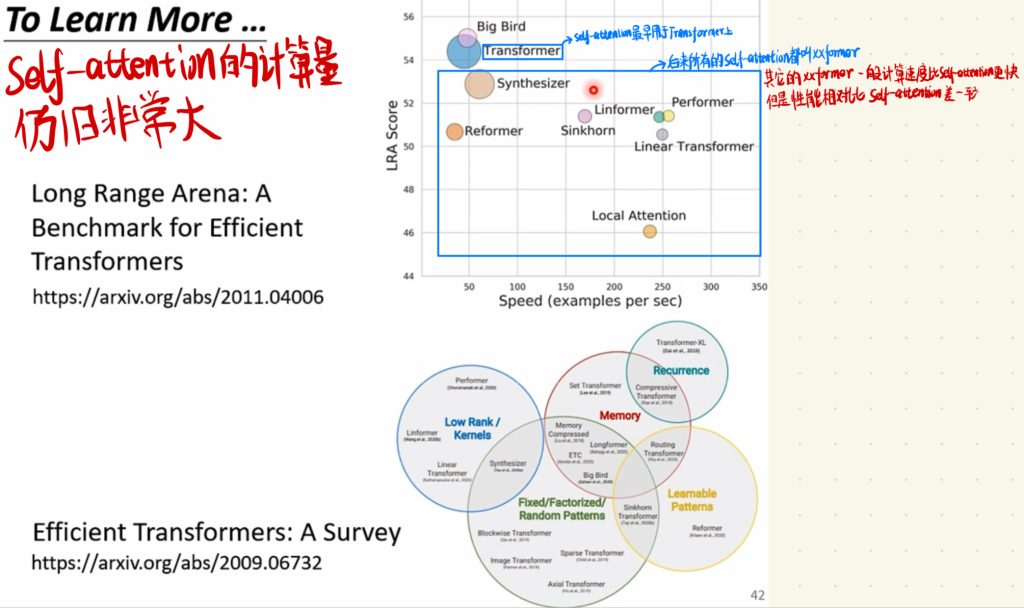
但是,其他改进的xxformer虽然计算速度比Self-attention本身更快,可是它们的性能都相对比Self-attention差一点。
以上就是关于自注意力机制(Self-attention)讲解的笔记。
