【决策树相关】吴恩达机器学习笔记EP10（P91-P100）

从今天开始我将学习吴恩达教授的机器学习视频，下面是课程的连接1.1 欢迎来到机器学习!_哔哩哔哩_bilibili。一共有142个视频，争取都学习完成吧。

---

选择拆分信息增益

上次介绍的熵其实本身不能很好的指导选择拆分，真正指导分割的是由熵组成的信息增益。

下图是三个信息增益的计算过程，主要就是根节点的熵减去左右加权熵。

信息拆分也可以理解为熵的减小值。

如果熵的减小太少，可以在合适的时候选择不继续分裂。

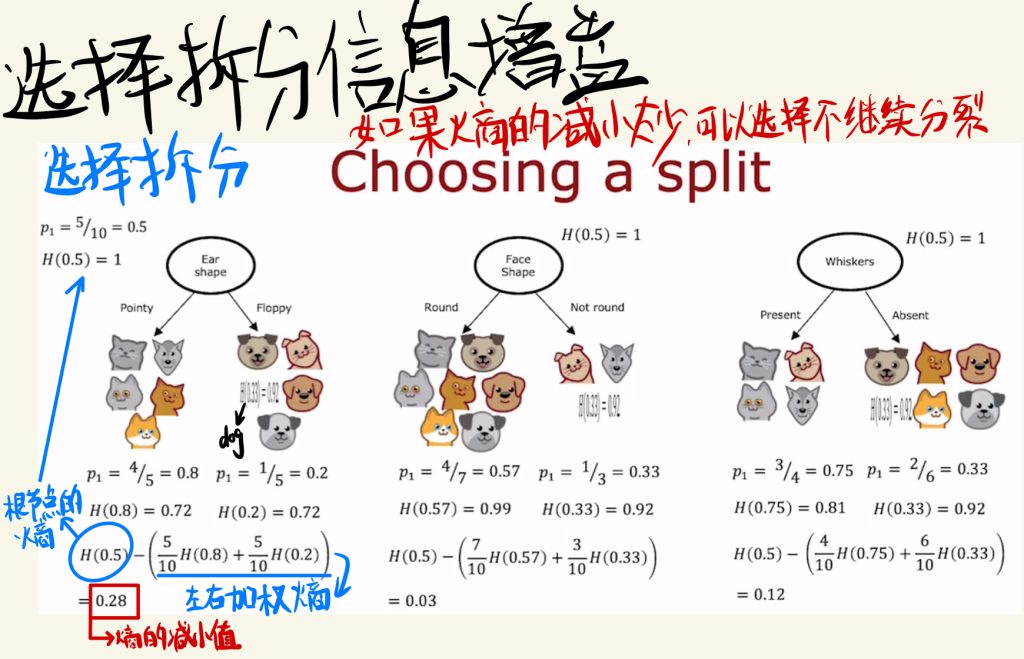
下面是信息增益的计算公式。

选择信息增益高的分类特征，有望提高数据子集的纯度。

整合

下面是整个学习树的学习过程：

从根节点开始。

计算所有可能特征的信息增益，选择最高的一个特征。

根据选择的特征对数据进行拆分为左右分支。

继续重复分割过程，直到满足之前说的停止条件：

当一个节点都是一个类时；当分割节点超过树最大深度时；额外分割的纯度低于某个阈值时；当一个节点中的样例数量低于某个阈值时。

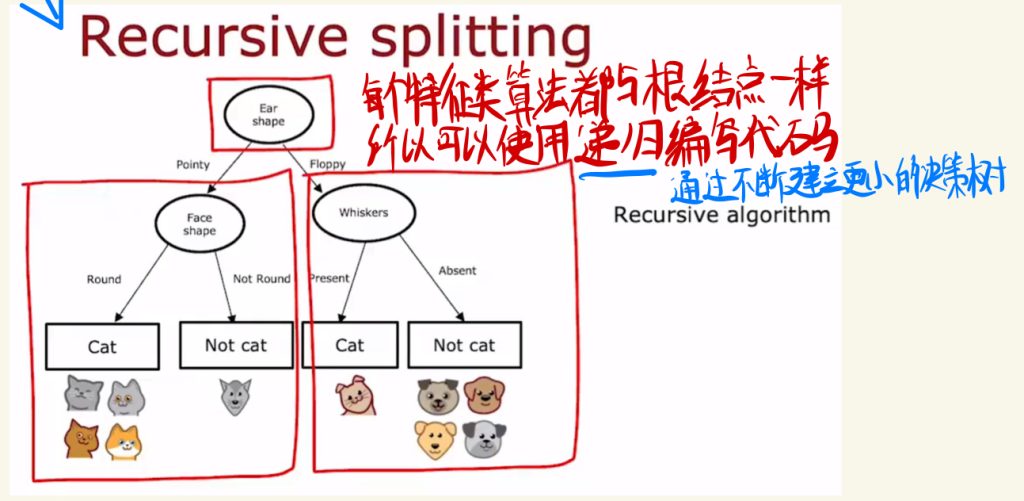
每个特征算法都与根节点一样，所以可以使用递归编写代码。（通过不断建立更小的决策树）

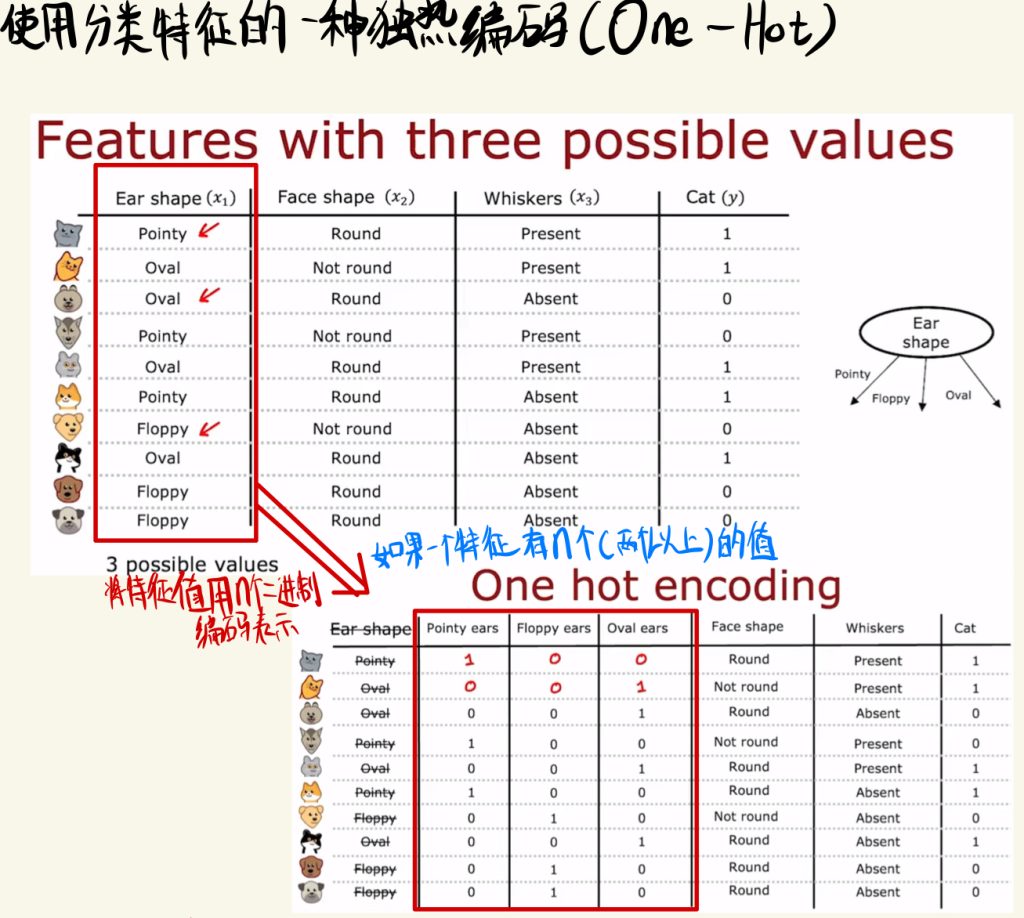
使用分类特征的一种独热编码（One-Hot）

如果一个特征有n个（两个以上）的值，要是推广跟之前一样的方法，就要分成三类，但是我们不必要这么做。

我们可以将特征值用n个二进制编码表示。

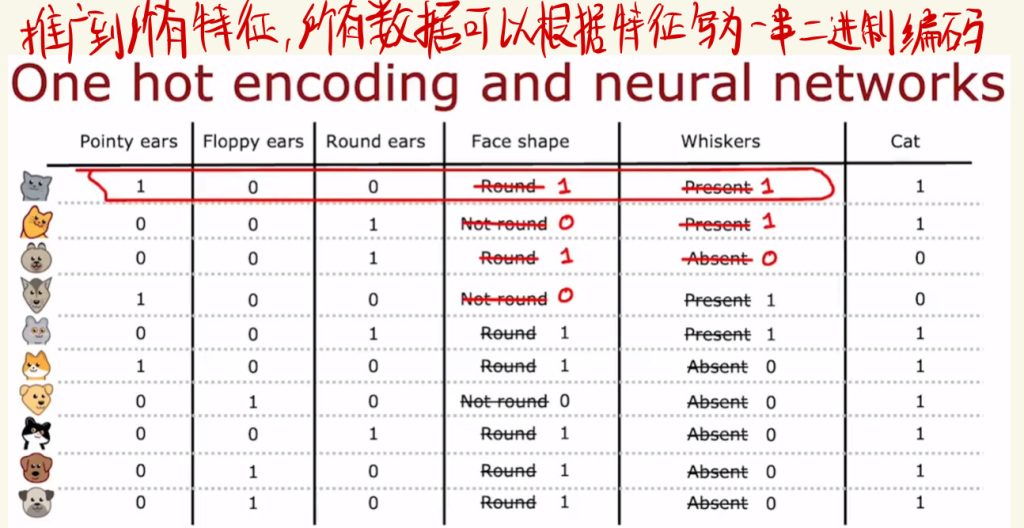
推广到所有特征，所有数据可以根据特征写为一串二进制编码。

连续的有价值特征

有些特征值（如体重等）是连续的，无法直接分裂数据。

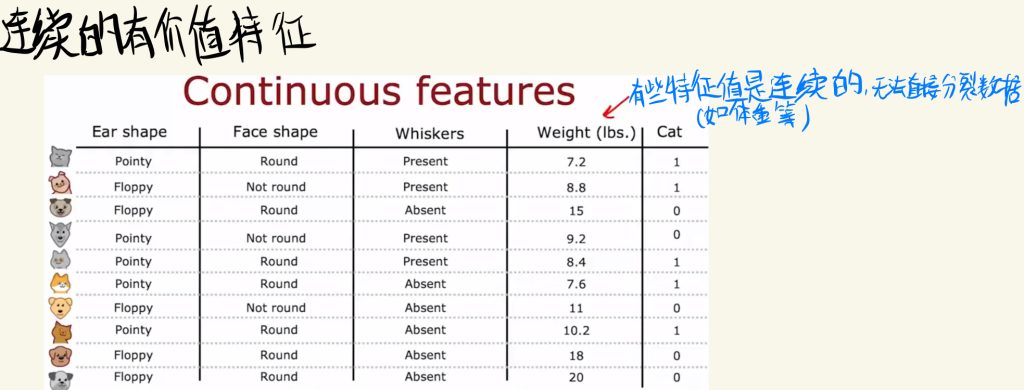
可以将连续的值分为是否大于某个阈值的两类。

然后尝试不同的阈值计算信息增益，选择一个信息增益最大的阈值。

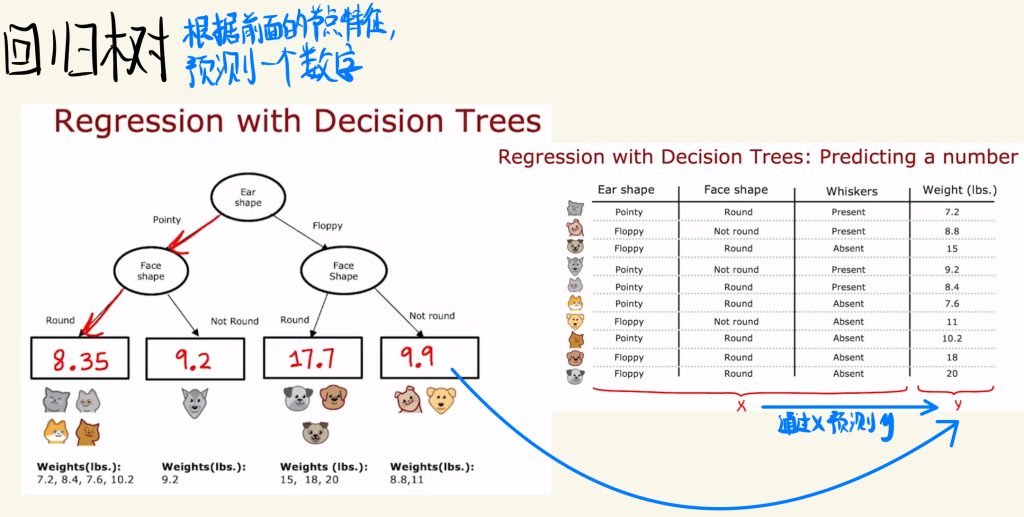
回归树

不仅有决策树，树也可以用于回归。

比如下面这种根据前面节点特征预测一个数字。

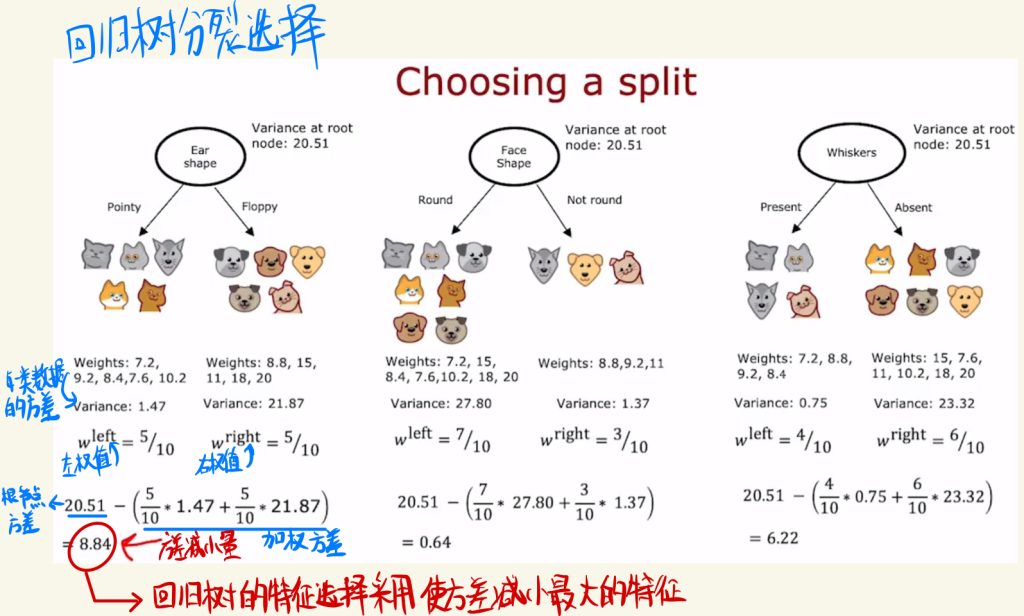
回归树分裂的选择和之前差不多。这里使用方差减小量去选择特征。

具体来说方差减小的计算就是用根节点方差减去左右加权方差。

回归树的特征选择采用使方差减小最大的特征。

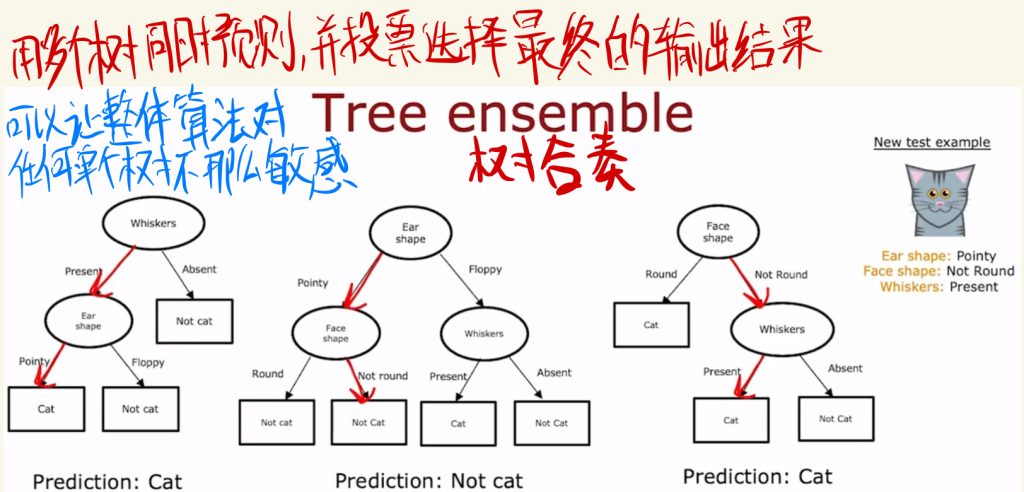
使用多个决策树

如下图例子所示，决策树对细小的数据改变都很敏感。

比如下面在数据集中只改了其中一个数据，但在不同决策树中的预测结果差异巨大。

用多个树同时预测，并投票选择最终的输出结果可以让整体算法对任何单个树不那么敏感。

如下面这种操作称之为树合奏。

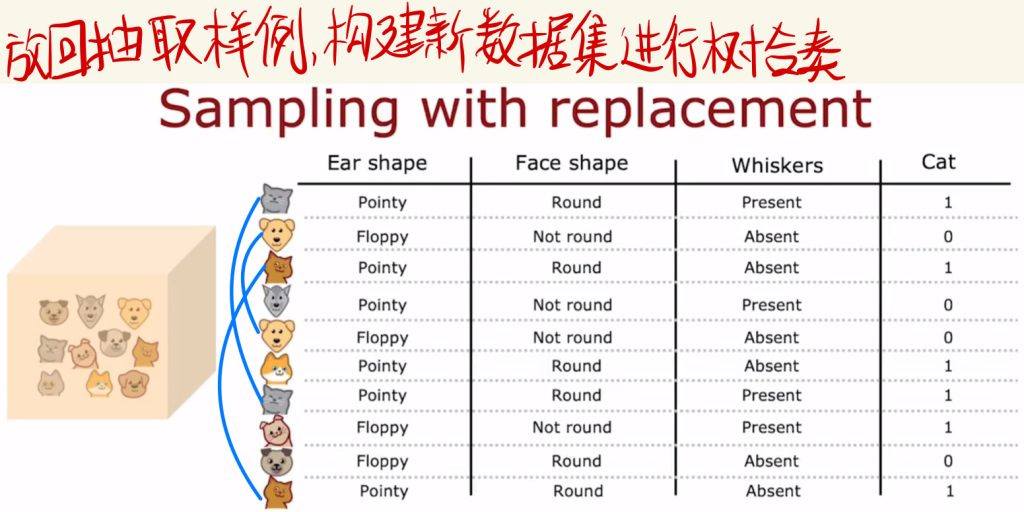
放回抽样

下面介绍一种随机抽样方法。

就是每次随机抽取一个样例，然后放回，再次抽取。

放回抽取样例，构建新数据集进行树合奏。

每次抽取到的样例当中有重复的也是可以的。

随机森林算法

然后介绍随机森林算法，下面使生成树样例：

先使用放回抽取一部分的数据，用这部分数据训练一个树。

然后以此类推，训练多个树。

每个树中的特征都不同，因为每次抽取到的数据不同，所以信息增益选择的分类特征也可能不同。

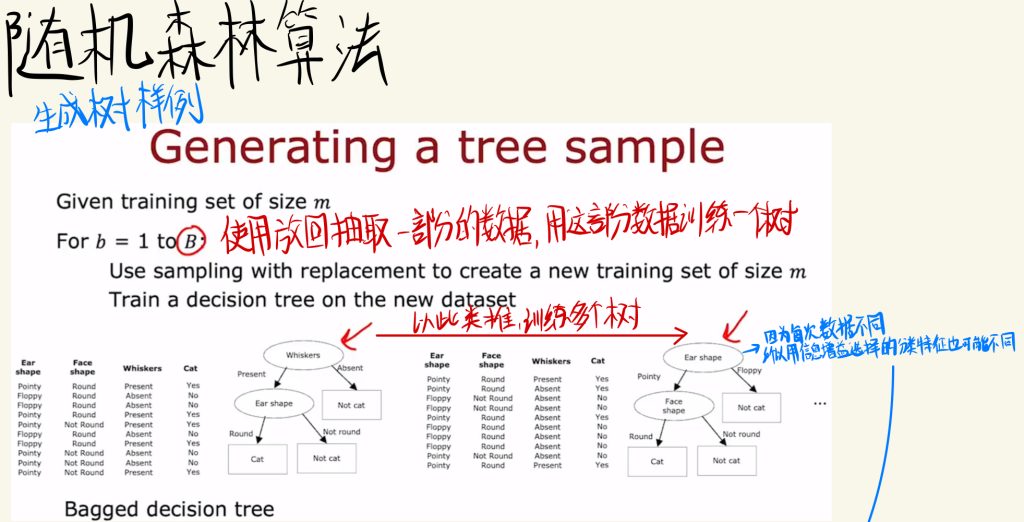
之后的特征抽取不必在所有特征中选择。

可以从k个小于特征总数n的特征当中选择特征。

一般n很大的时候，可以将k设成n的平方根。

XGBoost

XGBoost算法则更多地将注意力放在训练预测错误的数据上。

方法和之前差不多，但是在构建完一个决策树后，预测结果下一次放回抽取中预测错误的数据更容易被抽到，然后和随机森林一样，用新构建的数据集再次训练一个决策树。

决策树的具体算法有一点复杂，但是可以直接在对应的库中直接被调用。

# 分类中的使用
from xgboost import XGBClassifier

model = XGBClassifier()

model.fit(x_train, y_train)
y_pred = model.predict(x_test)

# 回归中的使用
from xgboost import XGBRegressor

model = XGBRegressor()

model.fit(x_train, y_train)
y_pred = model.predict(x_test)

什么时候使用决策树

最后是决策树与神经网络的对比。

决策树：

在结构化的数据中效果更好。

不建议在非结构化数据（如图像、音频、文本等）中使用。

训练速度更快。

小的决策树可能是人类可解释的。

神经网络：

可以很好地处理一切类型的数据。

可能比决策树慢。

适合迁移学习。

当构建一个由多个模型一同工作的系统时，神经网络更容易串起多个模型。