【多特征梯度下降相关】吴恩达机器学习笔记EP3（P21-P30）

从今天开始我将学习吴恩达教授的机器学习视频，下面是课程的连接1.1 欢迎来到机器学习!_哔哩哔哩_bilibili。一共有142个视频，争取都学习完成吧。

---

多类特征

特征可以有多个，所以我们也可以像EP2里面一样对这些特征做索引变量。

在同一行索引i中，将里面所有的特征放到一个集合当中，这个集合称为向量。向量是一个数字列表。

如下图中的向量是一个行向量。

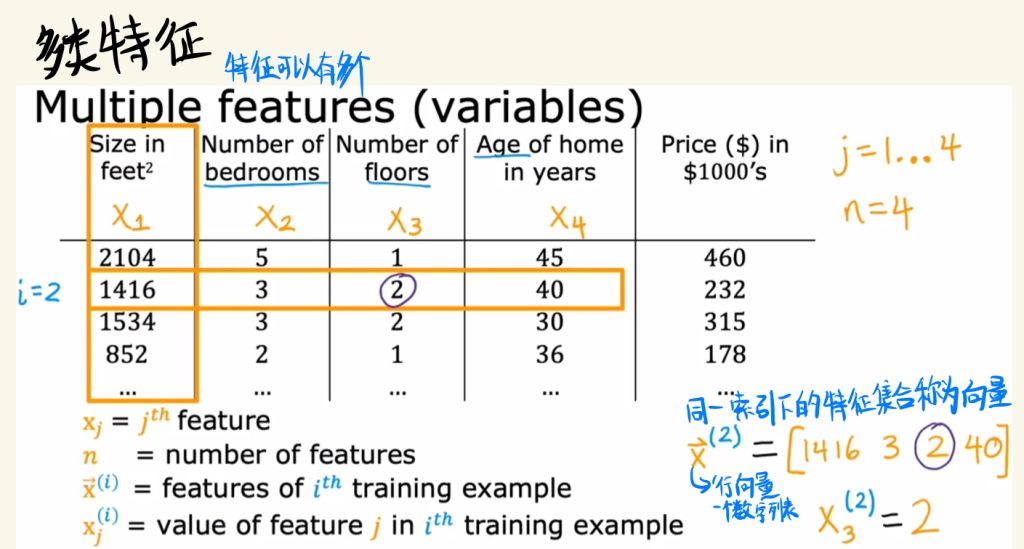
下面举例一个多类特征模型的写法。

将多个特征整合为一个向量可以简化模型的写法。

两个向量之间的对应的特征相乘然后将全部加起来的操作就是点乘。

下面这个模型也可以称为多元线性回归模型。

向量化不仅可以让代码更加简洁，还可以提高代码的运行速度。

因为处理向量的Numpy使用硬件并行计算技术加快了代码的运行速度。

因为向量化的计算是并行的，因此代码运行上更简洁高效。

下图是向量之间点乘的说明，可以看到特征之间采用同时并行计算。

多元线性回归的梯度下降法

多元线性回归的梯度下降法，仅将原本一个参数换成了一个向量。

在线性回归中的一种梯度下降法代替

在线性回归当中，正规方程也可以做到梯度下降的功能，无需迭代解决w和b。

但是它的缺点是不能用在其它学习算法中，而且在特征数很大（大于10000）时处理速度很慢。

所以梯度下降法完全优于正规方程，推荐使用梯度下降法，但是你又可能会在线性回归问题中看到正规方程的使用，只需了解即可。

特征缩放

有时候几个特征之间的取值范围差距较大。

选择合理的权重，一般特征值可能很大的，那么它的权值较小比较合理。

调整合理的特征大小，有助于梯度下降，有助于找到一条更直接的路径达到全局最小值。

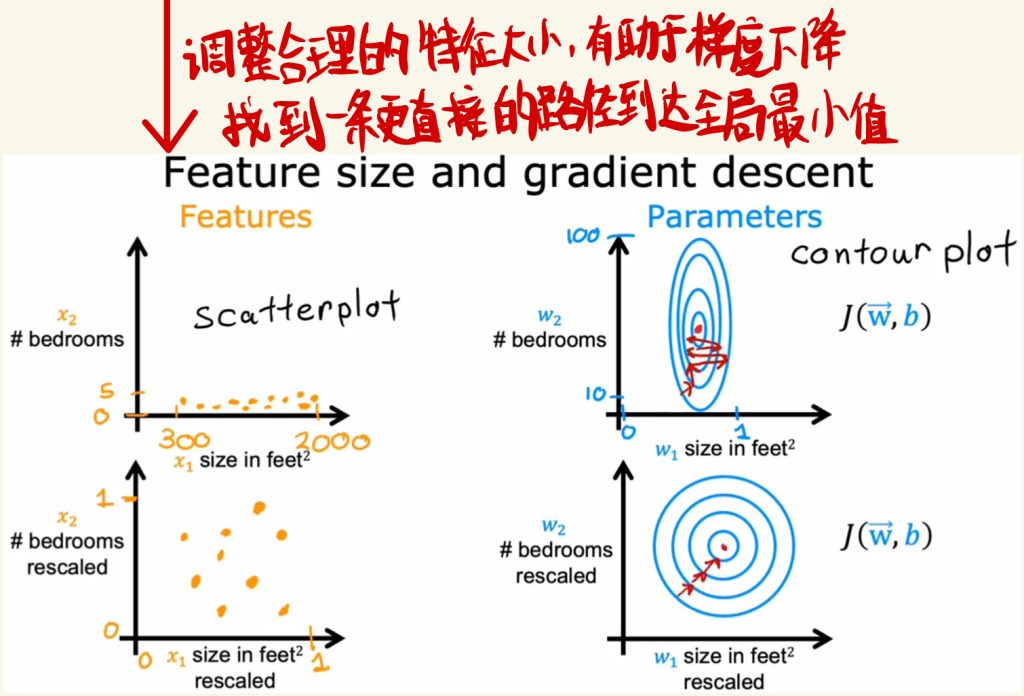
特征取值范围差距过大时，可以采用缩放以获取具有非常不同的值范围，将它们缩放成具有相互可比性的值范围。

下图是平均归一化和Z值归一化的示例。

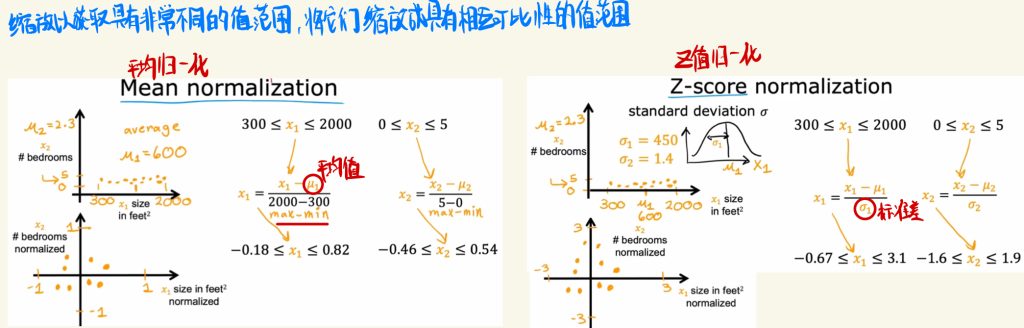
特征值范围相近是就无需进行缩放处理，或者说可选择处理。

特征值范围差过大或过小就需要进行缩放处理。

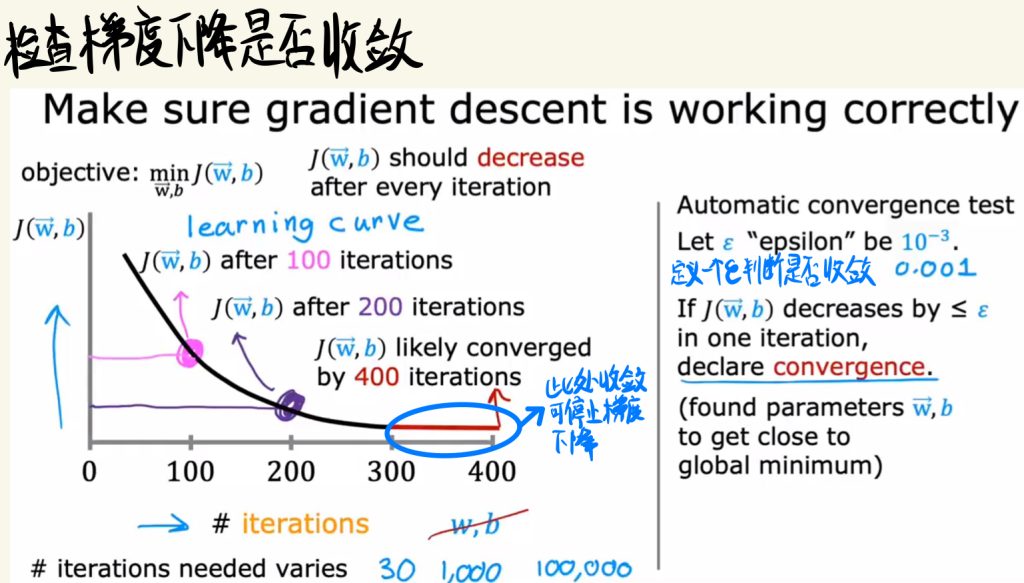
检查梯度下降是否收敛

可以定义一个ε来判断梯度是否收敛。如果收敛，可以停止梯度下降。

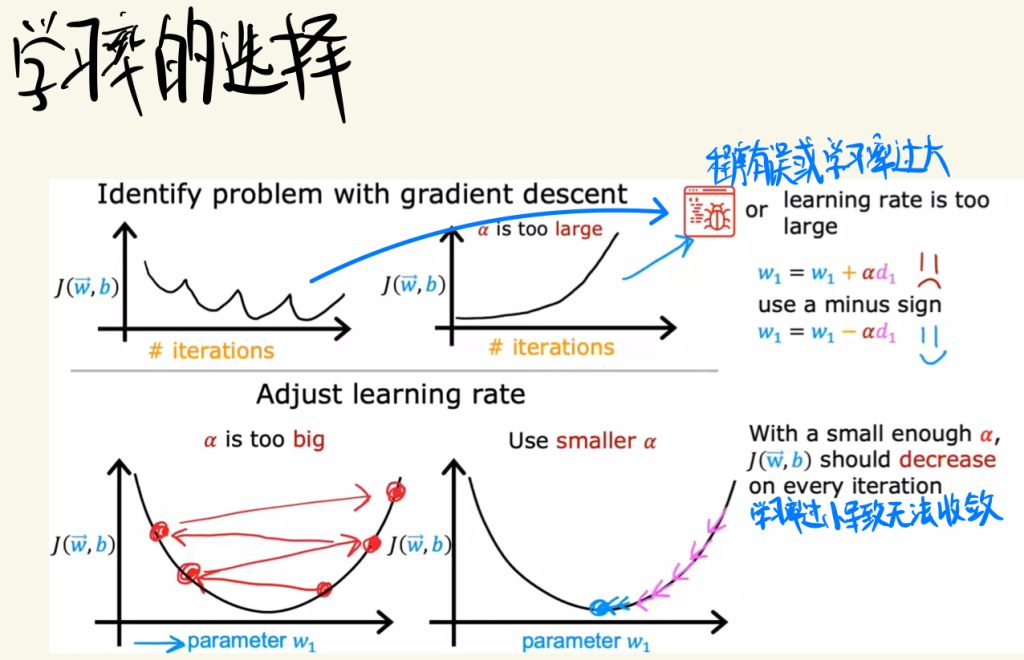
学习率的选择

学习率过大可能会产生如下图的曲线。

如果学习率过小会导致J函数无法收敛。

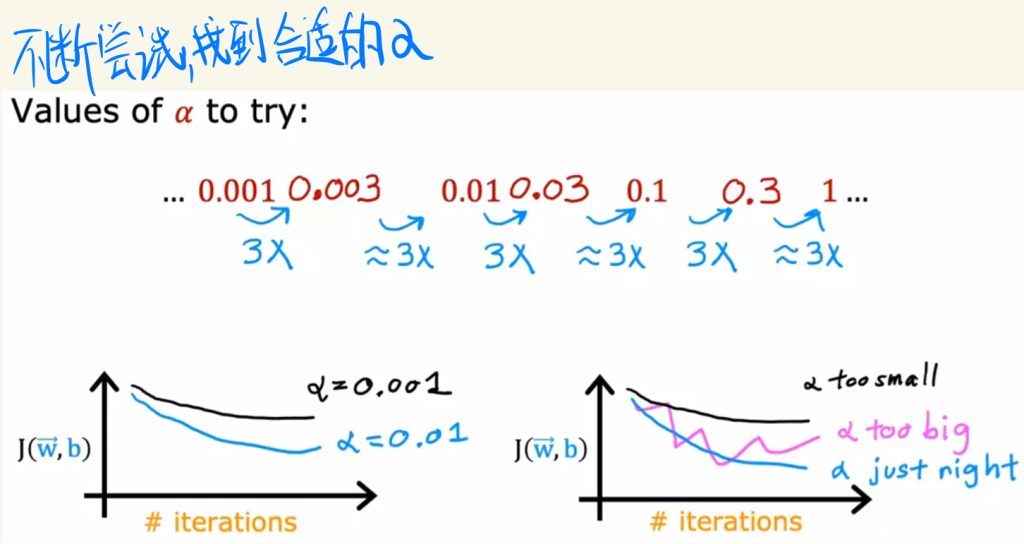
可以通过不断尝试，找到合适的学习率α值。

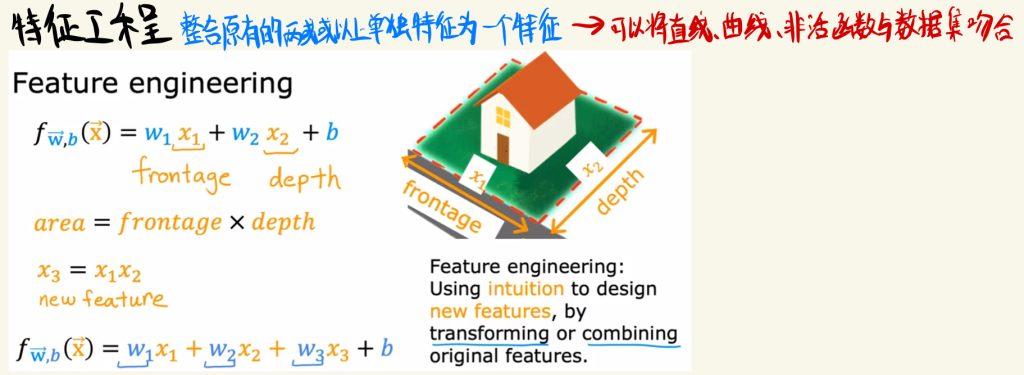
特征工程

特征工程就是整合原有的两个或以上单独特征为一个特征。这样可以将直线、曲线、非活函数与数据集吻合。

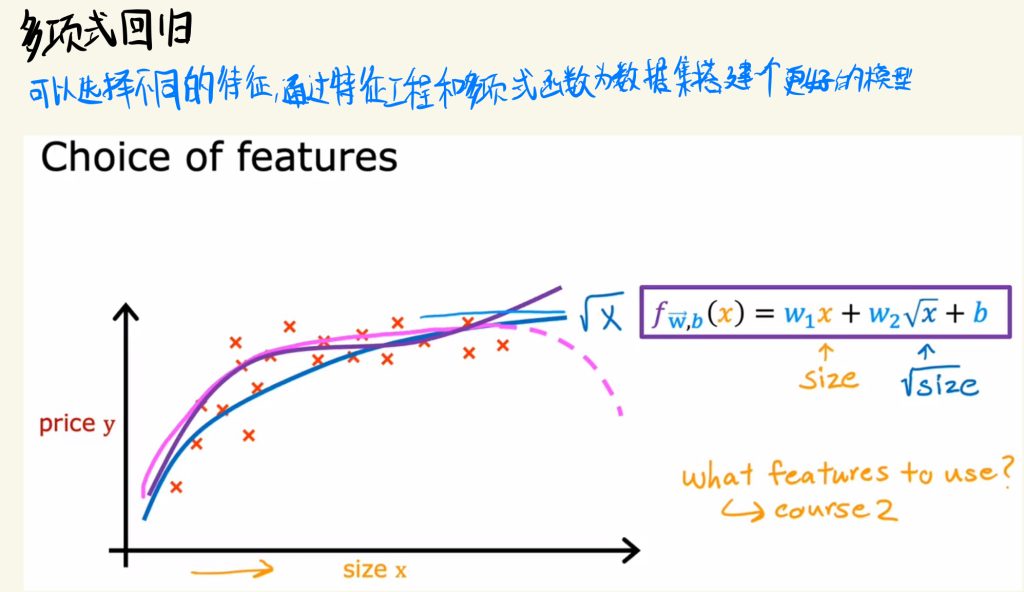
多项式回归

可以选择不同的特征，通过特征工程和多项式函数为数据集搭建一个更好的模型。